离散：0.图的概念和术语

图的概念：

1、图的定义：

一个图G=(V,E)由顶点的非空集V和边的集合E构成，每条边有一个或两个顶点与它相连，这样的顶点称为边的端点。边连接它的端点。

2、图的分类

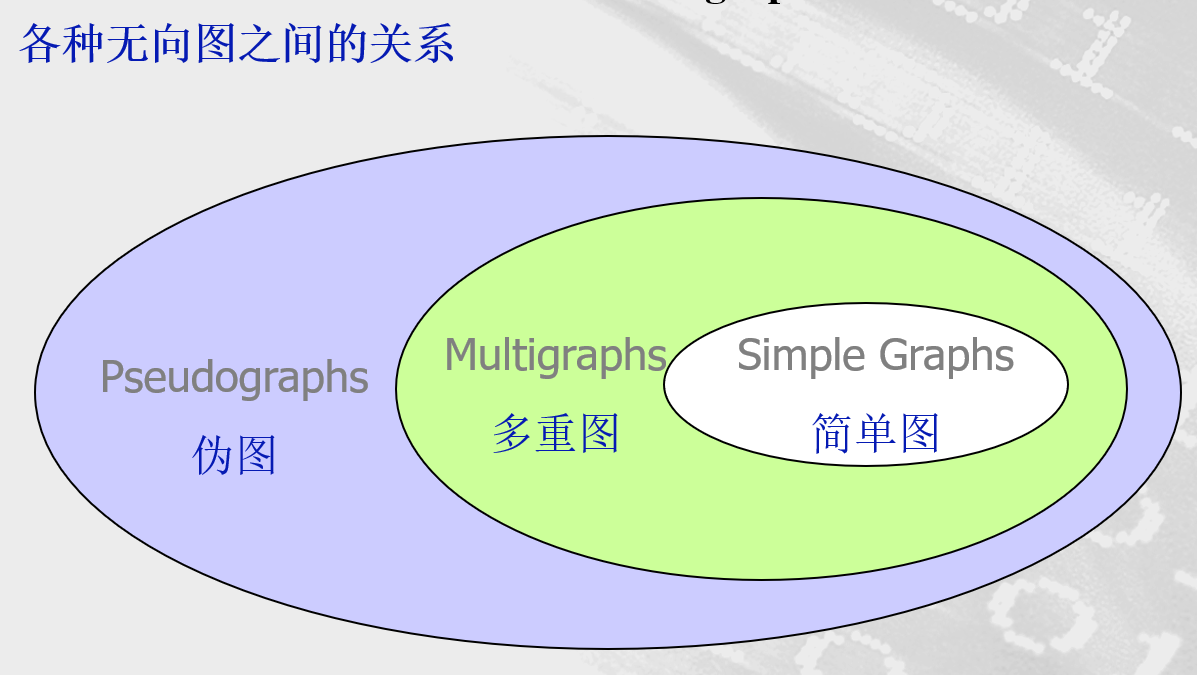
• 无向图
  • 简单图
    • 简单图G=(V,E)是由非空顶点集V（有穷集）和边集E所组成的，V的不同元素的无序对称为边。简单图不存在环，且两个顶点间最多只有一条边
  • 多重图
    • 在简单图的基础上，多重图允许顶点对之间有多重边
  • 伪图
    • 伪图也是多重图，它可以存在环

• 有向图

  • 有向图(V,E)是由非空顶点集V、边集E所组成的，边V中元素的有序对。允许有环(即相同元素的有序对)，但不允许在两个顶点之间有同向的多重边。

• 有向图

  • 简单有向图
  • 有向多重图
    • 有向多重图G=(V,E)是由非空顶点集V、边集E组成的,其中可以存在多重边
  • 混合图

图的术语：

degree of a vertex （顶点的度）

在无向图里顶点的度是与该顶点关联的边的数目，例外的情形是，顶点上的环为顶点的度做出双倍贡献

• 顶点v的度记做deg(v)

• If deg(v) = 0,v is called isolated 孤立的

• If deg(v) = 1, v is called pendant 悬挂的

定理一：握手理论

定理二

An undirected graph has an even number of vertices of odd degree. 无向图有偶数个奇数度顶点

有向图中的度

The in degree 入度 of a vertex v, denoted $deg^-(v)$is the number of edges which terminate at v

顶点v的入度是以v作为终点的边数。

Similarly, the out degree 出度 of v, denoted $deg^+(v)$, is the number of edges which initiate at v

顶点v的出度是以v作为起点的边数

定理三

Let G = (V, E) be a graph with direct edges. Then

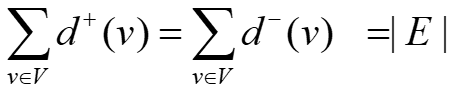
在带有向边的图里，所有顶点的入度之和等于出度之和。这两个和都等于图的边数。

一些特殊的简单图

• 完全图

  • n个顶点的完全图是在每对不同顶点之间都恰有一条边的简单图。通常用$K_n$表示

• 圈图$C_n$ (n>2)

  • 指n个顶点围成一圈的图

• 轮图$W_n$(n>2)

  • 当给圈图添加另一个顶点，而且把这个顶点与圈图里n个顶点逐个连接时，就得出轮图。

• 偶图（二分图）

  • 若把简单图G的顶点集分成两个不相交的非空集合$V_1$和$V_2$，使得图里的每一条边都连接着$V_1$里的一个顶点与$V_2$里的一个顶点，则G称为偶图。

子图：

设G是一个图，$E_1\subseteq E(G)$，以$E_1$为边集，$E_1$中边的端点全体为顶点集构成的子图，称为由$E_1$导出的G的子图(边导出子图)，记为G($E_1$)。

又设$V_1\subseteq V(G)$，以$V_1$为顶点集，端点均在$V_1$中的边的全体为边集，构成的子图，称为由$V_1$导出的G的子图(点导出子图)，记为G($V_1$)。