暑期机器学习引论

介绍

How to Define A Learning Problem:

What to learn

通俗来讲，我们希望通过计算机学习算法以及给定的 $x,f(x)$ 对找出准确或近似的 $f$ 函数。

Whether it has learned

Apparent error rate显然是不可以的，这就好比抄答案，没有意义。

True error rate 是最客观的。

Reinforcement Learning

强化学习的主要任务就是通过在环境中不断地尝试，根据尝试获得的反馈信息调整策略，最终生成一个较好的策略π，机器根据这个策略便能知道在什么状态下应该执行什么动作。

我觉得比较重要的几个观点：

RL is learning from trial and error interaction with the world.
RL is training by rewards and punishments.
增强学习的研究建立在经典物理学的范畴上，也就是没有量子计算也没有相对论。这个世界的时间是可以分割成一个一个时间片的，并且有完全的先后顺序，因此可以形成这样的状态，动作和反馈系列。这些数据样本是进行增强学习的基础。
另一个很重要的假设就是
「上帝不掷筛子！」
在增强学习的世界，我们相信如果输入是确定的，那么输出也一定是确定的。试想一下，有一个机械臂在练习掷筛子，以掷出 6 点作为目标。但是如果无论机械臂如何调整其关节的角度及扭矩，掷出的点数永远是随机的，那么无论如何也不可能通过算法使机械臂达成目标。因此，增强学习算法要有用，就是相信在增强学习中每一次参数的调整都会对世界造成确定性的影响。

马尔可夫决策过程（Markov Decision Processes,MDPs）

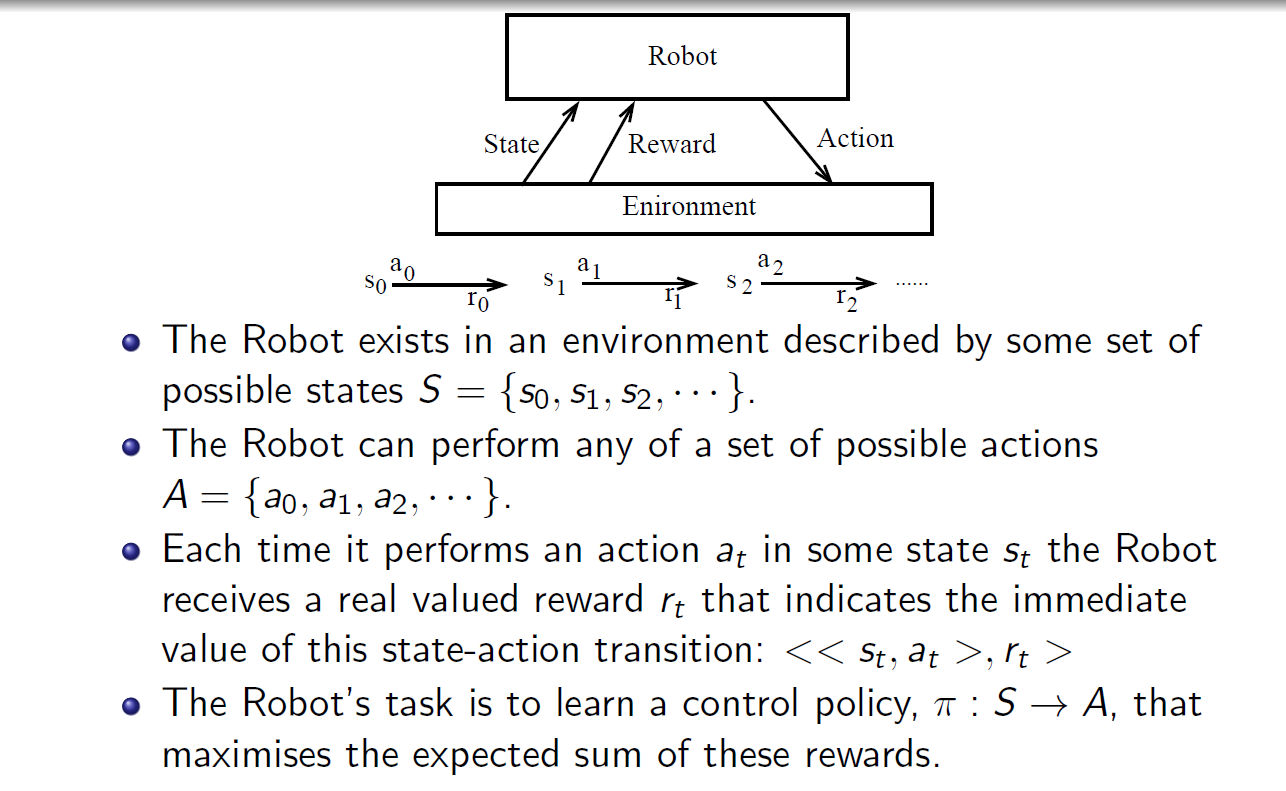
MDPs 简单说就是一个智能体（Agent）采取行动（Action）从而改变自己的状态（State）获得奖励（Reward）与环境（Environment）发生交互的循环过程。

MDP 的策略完全取决于当前状态（Only present matters），这也是它马尔可夫性质的体现。

其可以简单表示为： $M=<S,A,P_{s,a},R>$

基本概念

$s∈S$ ：有限状态 state 集合，s 表示某个特定状态
$a∈A$ ：有限动作 action 集合，a 表示某个特定动作
Transition Model $T(S,a,S')∼P_r(s'|s,a)$ ： Transition Model, 根据当前状态 $s$ 和动作 $a$ 预测下一个状态 $s'$ ，这里的 $P_r$ 表示从 $s$ 采取行动 $a$ 转移到 $s'$ 的概率
Reward $R(s,a)=E[R_{t+1}|s,a]$ ：表示 agent 采取某个动作后的即时奖励，它还有 $R(s, a, s’)$ , R(s) 等表现形式，采用不同的形式，其意义略有不同
Policy $π(s)→a$ ：根据当前 state 来产生 action，可表现为 $a=π(s)$ 或 $π(a|s)=P[a|s]$ ，后者表示某种状态下执行某个动作的概率

强化学习的本质是学习从环境状态到动作的映射（即行为策略）。而仅仅使用立即回报r(s,a)肯定是不够的(一个策略π的长期影响才是至关重要的).

回报（Return）：

$U(s_0 \,s_1\,s_2⋯)$ 与折扣率（discount） $γ∈[0,1]$ ： U 代表执行一组 action 后所有状态累计的 reward 之和，但由于直接的 reward 相加在无限时间序列中会导致无偏向，而且会产生状态的无限循环。因此在这个 Utility（效用）函数里引入 $γ$ 折扣率这一概念，令往后的状态所反馈回来的 reward 乘上这个 discount 系数，这样意味着当下的 reward 比未来反馈的 reward 更重要，这也比较符合直觉。定义

$U(s_0\,s_1\,s_2⋯)=∑_{t=0}^∞γ^tR(s_t), \,0≤γ<1\\ ≤∑_{t=0}^∞γ^tR_{max}=\dfrac{R_{max}}{1−γ}$

由于我们引入了 discount，可以看到我们把一个无限长度的问题转换成了一个拥有最大值上限的问题。

强化学习的目的是最大化长期未来奖励，即寻找最大的 U。（注：回报也作 G 表示）

基于回报（return），我们再引入两个函数

状态价值函数： $V(s)=E[U_t|S_t=s]$ ，意义为基于 t 时刻的状态 s 能获得的未来回报（reward ）的期望，加入动作选择策略后可表示为 $V_π(s)=E_π[U_t|S_t=s](U_t=R_{t+1}+γR_{t+2}+⋯+γ^{T−t−1}R_T)$
动作价值函数： $Q_π(s,a)=E_π[U_t|S_t=s,A_t=a]$ ，意义为基于 t 时刻的状态 s，选择一个 action 后能获得的未来回报（return）的期望

价值函数用来衡量某一状态或动作 - 状态的优劣，即对智能体来说是否值得选择某一状态或在某一状态下执行某一动作。

引出价值函数，对于获取最优的策略 Policy 这个目标，我们就会有两种方法：

直接优化策略或者使得回报更高；
通过估计 value function 来间接获得优化的策略。道理很简单，既然我知道每一种状态的优劣，那么我就知道我应该怎么选择了，而这种选择就是我们想要的策略。

当然了，还有第三种做法就是融合上面的两种做法，这也就是以后会讲到的 actor-critic 算法。

所以最开始的PPT的图也可以这样表示：

Value Function 价值函数

这部分主要引自：

https://zhuanlan.zhihu.com/p/21262246
https://zhuanlan.zhihu.com/p/21340755
https://www.zhihu.com/column/c_1297485212247425024

我们用一个例子来说明 Value Function 的含义与重要性。

这是一个投资决策问题：假如我们有一笔 X 美刀的资金，我们眼前有三种选择来使用这笔资金：

使用资金进行股票投资
使用资金进行买房投资
使用资金购买书籍，科研设备等提升资金

那么，我们就面临如何做选择的问题。这里假设我们只能选择其中的一个做选择。

我们先来解释一下直接基于 Policy 的方法是怎样的。

直接基于 Policy 的意思就是我们有一套 Policy 策略，我们基于这个策略进行操作，比如可以有如下所示的策略：

if 资金 X > 500000:
   选择股票投资
else if 资金 X > 100000:
   选择房产投资
else:
   选择买书，买设备自我提升

那么上面的伪代码就是表示一个极其简单的策略。这个策略只考虑资金量，输入资金量，输出决策方式。如果把 Policy 策略看做是一个黑箱，那么基于策略的方法就是：

那么如果不是基于 Policy 策略直接做出决策，我们还有什么办法呢？

显然有，而且大家可以从上面的简单策略看到一个最大的缺陷，就是上面的策略完全不考虑每一种选择未来的价值。我们做决策是有目的的，那就是为了最大化未来的回报 Result 是不是？那么对于上面的投资选择问题，我们的目标就是希望我们的投资回报率最高。因此，上面的简单策略竟然完全不考虑每一种选择的价值，而仅考虑资金量，显然是一种欠考虑的方法。因此，我们是不是应该评估一下每一种选择的潜在价值呢？耶，价值 Value 出来了，是不是？通过对价值的评估，我们也就可以有如下的做决策的方法：

我们就评估每一种状态（选择 + 资金量）的价值，然后选择价值最高的作为最后的决策。

比如说：

if 投资股市:
    因为股市低迷，价值为 - 100
if 投资房产 + 资金量 > 100000:
    因为房产泡沫还没破，各地房价还在涨，价值为 + 500
if 提升自己 + 资金量 < 100000:
    当前人工智能潜力巨大，资金又不算太大，投资自己价值为 + 1000
...(更多的评估价值的方法）

OK, 假设现在我们有 50000 的资金，那么根据我们的价值估算方法，选择投资自己的价值最大，为 + 1000，因此我们就选择投资自己作为决策结果。

从数学的角度，我们常常会用一个函数来表示一个状态的价值，也可以用来表示状态及某一个动作的价值。我们上面的例子就是来评估某一个状态下动作的价值，然后根据价值做出判断。实际上我们这里也是有策略的，我们的策略更简单：

1 2	if 某一个决策的价值最大：选择这个决策

这就是价值函数的意义。在后面的文章当中，我们还会发现，其实我们还可以同时使用策略加价值评估的方法来联合给出决策，这种算法就是所谓的「Actor-Critic」算法

为什么引出Value Function？
我们是为了得到最优策略，所以想通过评估状态的价值来引导决策。在MDP的世界，每个状态下的价值是确定的，即存在一个唯一的值来表示某一个状态。也就是说存在一个和策略无关的值来表示某一个状态。然后我们就可以利用这个状态的价值来进行决策。也就是说这里有一个先有鸡还是先有蛋的问题。我们是先有价值，还是先有策略。这里当然是先有价值，然后再进行决策。
但是，很显然，我们很难得到这个Value Function。要么是因为我们不是完全可观察的环境，要么就是我们根本无法计算这个Value Function。我们唯一能做的就是去估计这个Value Function。
怎么估计？
唯一的方法就是反复试验。
但是试验的过程中我们肯定得采取某一个策略，否则试验进行不下去。因此我们得到的reward都是在这个策略之下得到的，所以我们得到的value function显然也就是在这个策略下得到的value function。这只是实际得到的value function。
因此，我们就想，如果使用不同的策略进行无数次的实验，然后把最大的value function作为真正的value function。这样可以吗？这样当然可以啊。因为最大的value function肯定是唯一的。我们保证了唯一性，也就是可以基于这个来做判断。而使用最大值其实也是显而易见的，代表这这个状态的最大可能。既然每个状态的最大可能价值知道了，我们也就可以根据这个最大可能价值来做判断，得到的策略也就是最优策略Optimal Policy。这就实现了我们的初衷：得到状态的价值Value Function。

Bellman方程

没错，就是算法课讲的那种Bellman方程（编者注）

在上文我们介绍了Value Function价值函数，所以为了解决增强学习的问题，一个显而易见的做法就是----

我们需要估算Value Function

是的，只要我们能够计算出价值函数，那么最优决策也就得到了。因此，问题就变成了如何计算Value Function？

怎么估算价值呢？

我们还是先想想我们人是怎么估算的？我们还是以上面的投资决策问题来作为例子

一般我们基于以下几种情况来做评估：

其他人的选择。比如有很多人投资股市失败，因此我们就会降低我们投资股票的价值。
自己的反复试验。我们常常不是只做一次选择，而是做了很多次选择，从而收获了所谓的“经验”的东西。我们根据经验来评估选择的价值。比如我们做了好几次投资楼市的选择，结果大获成功，因此我们就会认为投资楼市是不错的选择。
基于理性分析。我们根据我们已有的知识对当前的情况做分析，从而做出一定的判断。
基于感性的逻辑。比如选择投资自己到人工智能领域。虽然我们大约觉得人工智能前景很好，但是我们真正要投资自己到这个领域有时候仅仅是出于一种热爱或者说一种理想主义。就是不管别人觉得好不好，反正我觉得好，我就这么选了。

计算机要如何才能评估价值呢？

其他人的选择。不好意思，计算机只有自己，没有其他人。也许你会说多台计算机。如果是共用一个“大脑”做分布式计算，那还是只有自己。
基于理性分析。不好意思，计算机在面对问题时往往什么都不知道，比如基于屏幕玩Atari游戏，计算机压根不知道看到的像素是个什么东西。它没有人类的先验知识，无法分析。（当然啦，先使用监督学习然后再增强学习的AlphaGo就是有先验知识的情况下做的增强学习）
基于感性的逻辑。不好意思，计算机目前还产生不了感性。

那么，基于自己的反复试验呢？耶，这个可以啊。计算机这方面比人类强多了，可以24小时不分昼夜的反复试验，然后对价值做出正确的判断。

所以，Value Function从分析上是可以评估出来的，那具体该怎么评估呢？

我们下面将不得不引入点数学公式，虽然也会非常好理解。

还记得回报Result的基本定义吗？就是所有Reward的累加（带衰减系数discount factor）

$G_t=R_t+\lambda R_{t+1}+\ldots=\sum_{k=0}^\infty\lambda^kR_{t+k}$

那么Value Function该如何定义？也很简单，就是期望的回报啊！期望的回报越高，价值显然也就越大，也就越值得去选择。用数学来定义就是如下：

$v(s)=\mathbb E[G_t|S_t=s]$

接下来，我们把上式展开如下：

$\begin{aligned} v(s) &=\mathbb E[G_t|S_t=s] \\ &=\mathbb E[R_{t}+λR_{t+1}+λ^2R_{t+2}+...|S_t=s]\\ &=\mathbb E[R_{t}+λ(R_{t+1}+λR_{t+2}+...)|S_t=s]\\ &=\mathbb E[R_{t}+λG_{t+1}|S_t=s]\\ &=\mathbb E[R_{t}+λv(S_{t+1})|S_t=s] \end{aligned}$

因此，

$v(s)=\mathbb E[R_{t}+λv(S_{t+1})|S_t=s]$

上面这个公式就是Bellman方程的基本形态。从公式上看，当前状态的价值和下一步的价值以及当前的反馈Reward有关。

它表明Value Function是可以通过迭代来进行计算的

迭代与Q-learning 算法

考虑下面这个简单的迷宫问题:

从入口(Start)走到出口(Goal)就算胜利. 小方格的位置就是我们状态S, 行为Action只有四种(上下左右), 回报函数就定为每远离一步Goal, 回报-1.

价值迭代

如果使用价值迭代算法，我们更新每个状态 $s$ 的长期价值 $V(s)$ ，这个价值是立即回报 $r(s,a)$ 与下一个状态 $s+1$ 的长期价值的综合(想想是不是很有道理?)，从而获得更新:

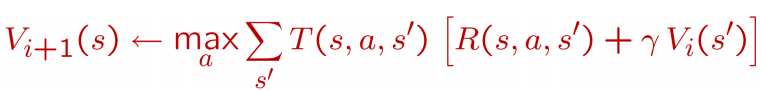
有两个点要注意:

每次迭代, 对于每个状态 $s$ , 都要更新价值函数 $V(s)$
对于每个状态 $s$ 的价值更新, 需要考虑所有行动Action的可能性, 这就非常消耗时间.

最后可以训练出所有状态s的价值, 大概是下面这样:

值得注意的是, 如果价值迭代完成后, 每个状态下一步的策略也就有了(选下一步价值较高的格子走, 就可以了)

策略迭代

如果使用收敛较快的策略迭代算法, 每次迭代我们分两步走:

第一步: 先任意假设一个策略 $π_k$ , 使用这个策略迭代价值函数直到收敛,

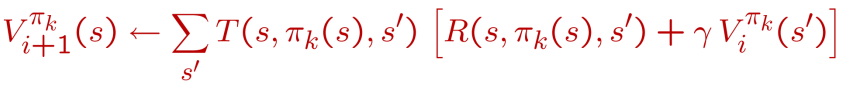
最后得到的 $V(s)$ 就是我们用策略 $π_k$ , 能够取得的最好价值函数 $V(s)$ 了(其实是策略的一种评估)

第二步: 我们重新审视每个状态所有可能的行动Action, 优化策略 $π_k$ , 看看有没有更好的Action可以替代老的Action:

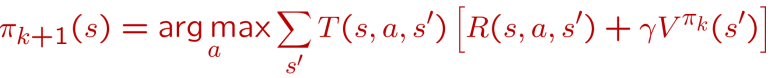
这样就最终优化了策略函数 $π_k$ 最终效果大概是这样的:

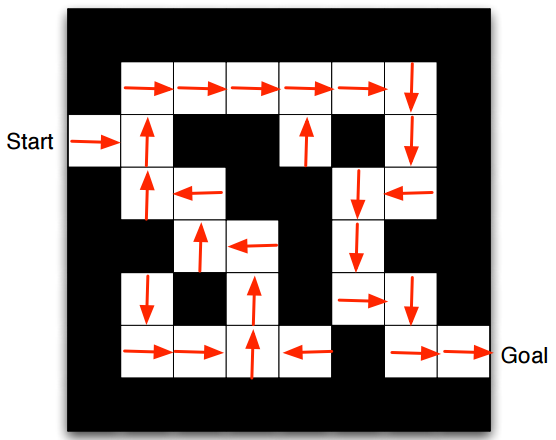
这就是策略迭代, 最后得到了每个状态应有的最佳策略.

正如我们开头说的, “是先用自己的”套路”边试边学, 还是把所有情况都考虑之后再总结”, 正是策略迭代与价值迭代的区别, 我们需要权衡考虑。

Q-Learning

发现原文好像不允许转载，好吧（我上面好像已经抄了好多了呜呜呜）

放上链接

https://zhuanlan.zhihu.com/p/21378532

https://blog.csdn.net/itplus/article/details/9361915

Q-Learning属于强化学习的经典算法，用于解决马尔可夫决策问题。为无监督学习。我们首先要对上面提到的价值函数的迭代有一定的理解而在此基础上进行迭代，当然很注重要的一点是，迭代是要有越来越好的趋势的，每次迭代都可以看作是一次学习或者改进。

盗一张策略迭代的图，很形象。

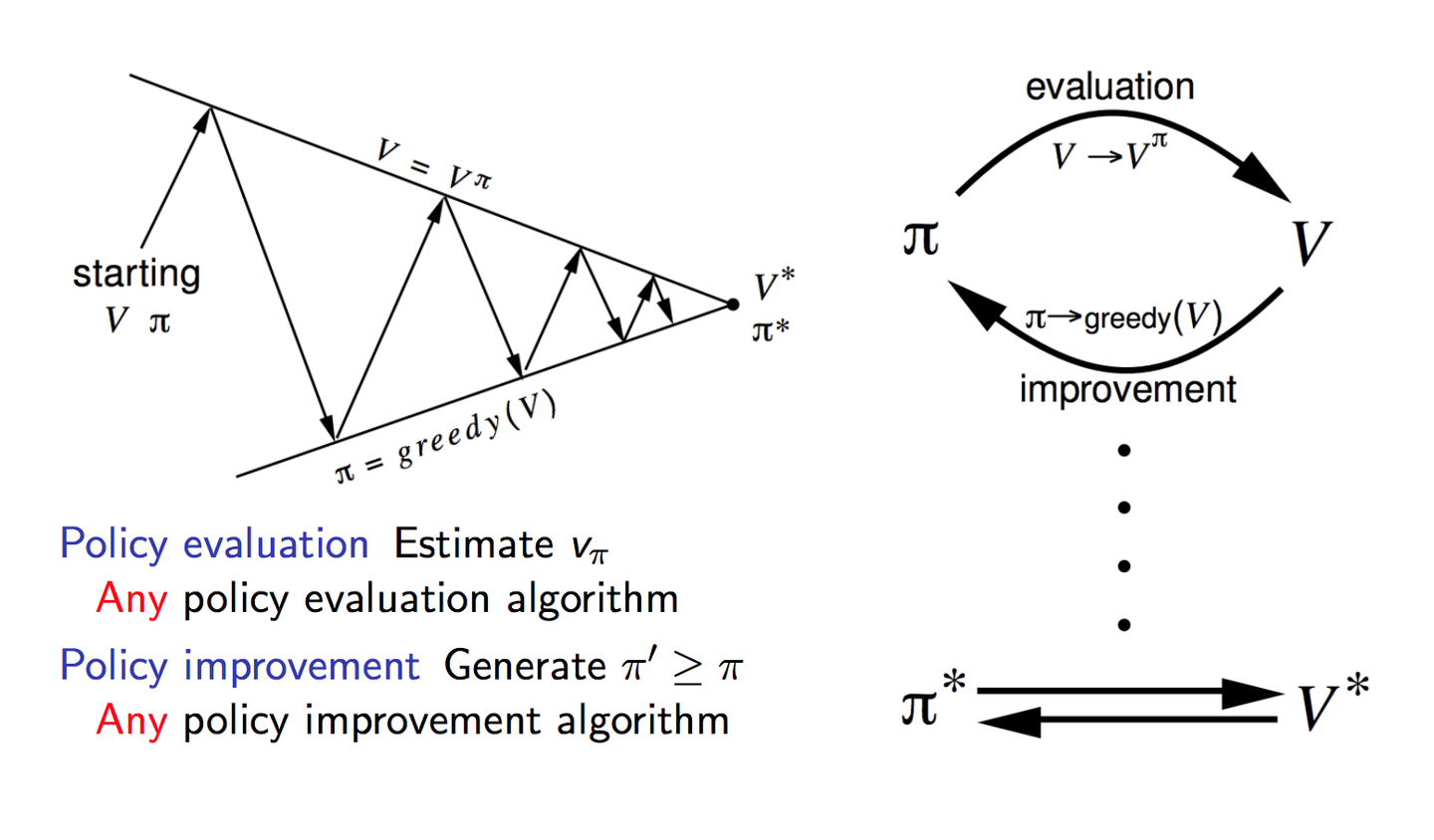
Q-values&Q-learing

(两种价值函数的关系)。也就是说我们要采取使得Q最大的action作为对应state下的 $V(s)$ 。

例如：

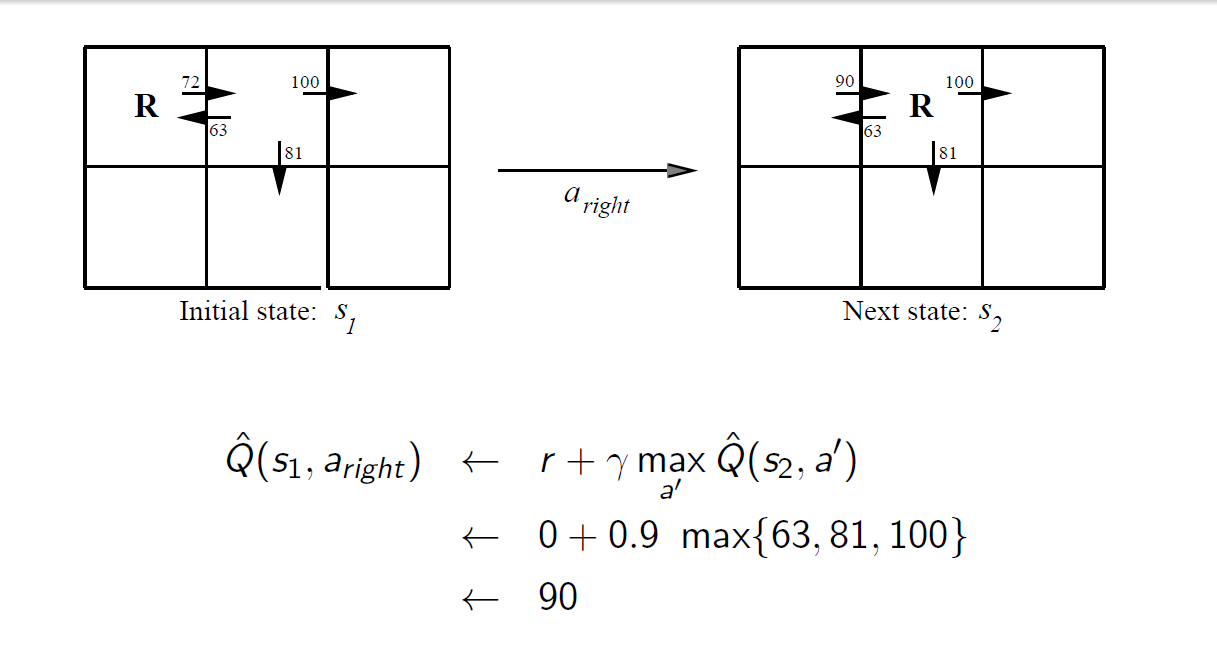
从状态 $s_1$ 进入 $s_2$ ，回报为0（我们认为只有到达终点时才会有回报），在 $s_2$ 时可以采取三种策略，最大的效用值为100，计算新Q值并赋值

参考

https://zhuanlan.zhihu.com/p/25319023
http://nooverfit.com/wp/15-增强学习101-闪电入门-reinforcement-learning/
https://zhuanlan.zhihu.com/p/21262246
https://zhuanlan.zhihu.com/p/21340755
https://www.zhihu.com/column/c_1297485212247425024

概念学习

概念学习是指从有关某个布尔函数的输入输出训练样例中推断出该布尔函数。这里假设并限定了目标函数是布尔函数。另外，这是一个由特殊向一般的过程。
如果把概念学习看做是一个搜索过程，范围是假设的表示所隐含定义的整个空间。搜索的目标就是为了寻找能最好地拟合训练样例的假设。
在心理学中，概念学习就是学习把具有共同属性的事物集合在一起并冠以一个名称，把不具有此类属性的事物排除出去。学习的过程具有排他性。由此，也可以看出为什么ML中的概念学习总表示为一个布尔函数（排他性，不是即非啊）。
归纳学习假设：任一假设如果在足够大的训练样例中很好地逼近目标函数，它也能在未见实例中很好地逼近目标函数。
概念学习可以看作是一个搜索过程，范围是假设的表示所隐含定义的整个空间。搜索的目标是为了寻找能最好地拟合训练样例的假设。

大部分的人类学习都包含了从过去的经历中获得一般性的概念。例如，人类可以通过在大量特征集合中定义出的特定特征集合，来辨别出每一种交通工具的不同。这个特征集合可以从 “交通工具” 的集合中区分出名为 “汽车” 的子集。而这种区分出汽车的特征集合便被称之为 “概念”。

类似地，机器也可以从概念中学习，通过处理旧数据/训练数据，找出对象是否属于特定类别，最终找出与训练实例拟合度最高的假设。

当然，老师提到了这样一句话我觉得很简单但是很重要，就是：Exactly you just remember given examples, you didn’t really learn. 也就是说我们的学习结果应该对未知的样例也有较为贴合实际的输出

概念

定义一个概念的项目/对象集称为实例集/实例空间，用 X 表示。

要学习的概念或函数称为目标概念，用 c 表示。它可以看作是一个在 X 上定义的布尔值函数，表示为 $c: X \rightarrow \{0, 1\}$ 。

具有特定目标概念 c 的特征的训练实例用 D 表示，其中训练实例的样式为 $<x,c(x)>$ ，那么学习者面临的问题则是去估计可在训练数据上定义的 c。

关于目标概念的特征，H 被用来表示学习者可能考虑的的所有可能假设的集合。此时学习者的目标是找到一个能够辨别 D 中所有对象的假设 H，使得对所有的 D 中的 x，每个模型h in H都表示一个生成之为0, 1函数,（即 $h: X \rightarrow\{0, 1\}$ ），都有 h(x) = c(x)。

一个支持概念学习的算法需要：

训练数据（通过过去的经验来训练我们的模型）
目标概念（通过假设来辨别数据对象）
实际数据对象（用于测试模型）

一些符号

每个数据对象都代表一个概念和假设。我们认为这样的一个假设 <true，true，false，false> 是更具体的，因为它只覆盖了一个实例。一般来说，我们可以在这个假设中加入一些符号。我们有以下符号：

ⵁ （一个拒绝所有实例的假设）
?（一个接受所有实例的假设）
< ? , ? , ? , ? > （全部接受/肯定）
<ⵁ, ⵁ, ⵁ , ⵁ >（全部拒绝/否定）

< ? , ? , ? , ? > 会接受所有的数据实例。? 符号表示此特定特征的值不会影响结果。

比如，判断一个同学是否喜欢机器学习课程：

那么对于假设集合H，其中每个假设h的每个属性要么是？或ⵁ，要么是其可选值的一个。

给定的一个训练样例可以是：

所以对于所有具体取值，合法的假设一共有 $3\times2\times2\times2\times2=48$ 个，即 $H=\{h_1,h_2...,h_{48}\}$

或者，更准确的说，我们的实例空间（Instance space）有48个。

那么对于这48个假设，每个都可能进入最后的结果集H或者不进入，对应的无偏假设空间共有 $2^{|H|}-1=2^{48}-1$ 个元素。（当然，结果集非空）

句法上不同的假设空间（Syntactically different hypothesis space）一共有 $5\times4\times4\times4\times4=1280$ 个。因为每个属性的取值除了特定值之外还有空值 ⵁ 与任意值？

语义上不同的假设空间（semantically different hypothesis space）一共有 $4\times3\times3\times3\times3+1=325$ 个，因为对于空值 ⵁ 我们明确知道这是被拒绝的，所以我们没有必要去进行任何学习，所以可以在每个属性中被直接剔除。

这其中的1对应的就是存在空集的情况，可以直接输出为false

所以我们可以只针对这325种情况进行考虑，大大降低了复杂度。

这325个才是我们真正应该关心的，通常选作假设空间（Hypotheses space）。

我们发现通过引入？这种形式我们假设空间的元素数要多于只考虑具体取值的实例空间的元素数，这其实说明我们假设空间的泛化能力要优于实例空间。
另一方面，∅在机器学习中是一个非常容易令人误解的概念, 我们可以尽量不去理它，所以325与324都是可以接受的。

Whenever getting stuck, consider the following:

Generalization:
Remove some constraints
Introduce new variables
Introduce disjunctions
Specialization:
- Add some constraints
- Instantiate variables with specific values
- Introduce conjunctions

FIND-S算法：寻找极大特殊假设

对于所有样本空间中的positive样本进行学习，对反例不做处理。

将 h 初始化为 H 中最特殊的假设（即 <ⵁ,ⵁ,ⵁ,…,ⵁ>）。
对每一个正例 x，对 h 的每一个属性约束 $a_i$ ，如果 x 满足 $a_i$ 那么不做任何处理；否则将 h 中 $a_i$ 替换为 x 满足的下一个更一般约束。

就是一个松弛的过程。

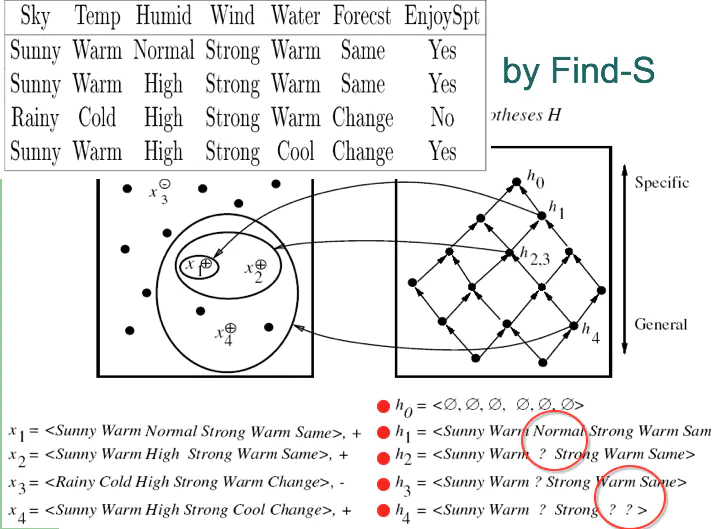
算法的局限性

用于概念学习的 Find-S 算法是机器学习最基本的算法之一，但它也具有如下的不足和缺点：

没有办法确定最终假设（Find-S 找出的）是否是唯一一个与数据一致 (consistent) 的假设。
不一致 (inconsistent) 的训练实例会误导 Find-S 算法，因为它忽略了 “负” 数据实例。一个能检测训练数据不一致的算法是更好的选择。
一个好的概念学习算法应该能够回溯对找到的假设的选择，以便能够逐步改进所得到的假设。但不幸的是，Find-S 不能提供这样的方法。

同时我们也很容易发现，在学习的过程中我们会出现算法结果趋向于 $<?,?,...,?>$ 的形式，但这一般是样本空间过于杂乱造成的（当然也可能是因为太大），这其实反映出样本空间中并无清晰的规律可言，也就是说是没有学习价值的。另一方面我们也可以通过细化属性的取值来缓解这一问题。

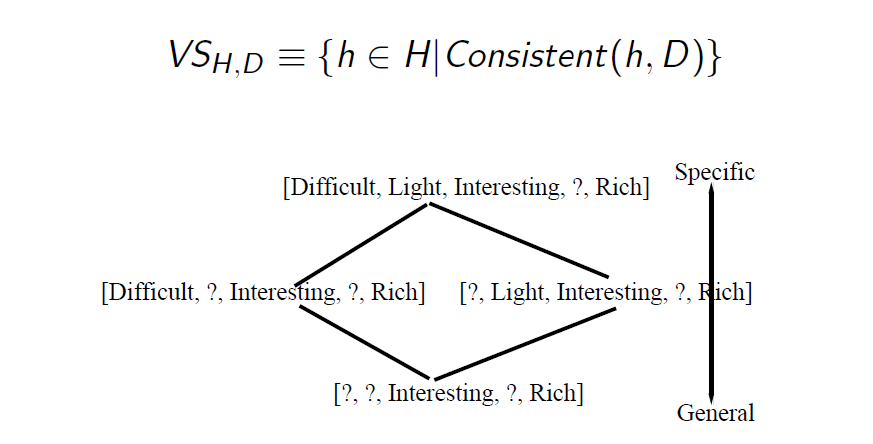
Version Space&Consistent

Consistent(全体正确性): a hypothesis h is consistent only if $h(x) = c(x)$ for each training example $<x, c(x)>$ in D

Version Space: The version space, denoted $VS_{H,D}$ , with respect to hypothesis Space $H$ and training examples $D$ , is the subset of hypotheses from $H$ consistent with the training examples $D$ .

归纳偏置

在机器学习中，很多学习算法经常会对学习的问题做一些关于目标函数的必要假设，称为归纳偏置 (Inductive Bias)。

归纳 (Induction) 是自然科学中常用的两大方法之一 (归纳与演绎，Induction & Deduction)，指从一些例子中寻找共性、泛化，形成一个较通用的规则的过程。偏置 (Bias) 则是指对模型的偏好。

通俗理解：归纳偏置可以理解为，从现实生活中观察到的现象中归纳出一定的规则 (heuristics)，然后对模型做一定的约束，从而可以起到 “模型选择” 的作用，类似贝叶斯学习中的 “先验”。
西瓜书解释：机器学习算法在学习过程中对某种类型假设的偏好，称为归纳偏好，简称偏好。归纳偏好可以看作学习算法自身在一个庞大的假设空间中对假设进行选择的启发式或 “价值观”。
维基百科解释：如果学习器需要去预测 “其未遇到过的输入” 的结果时，则需要一些假设来帮助它做出选择。
广义解释：归纳偏置会促使学习算法优先考虑具有某些属性的解。

例如，深度神经网络就偏好性地认为，层次化处理信息有更好效果；卷积神经网络认为信息具有空间局部性 (Locality)，可用滑动卷积共享权重的方式降低参数空间；循环神经网络则将时序信息考虑进来，强调顺序重要性；图网络则认为中心节点与邻居节点的相似性会更好引导信息流动。

事实上，将 Inductive Bias 翻译成归纳性偏好可能更符合我们的理解和认知。

最后一点很有意思，它指出任何无偏归纳算法都只是相当于记住了训练集，相当于没有学习，对其他的样本没有任何可用性。这其实反映了归纳偏置的一个特点或意义，即：归纳偏置的意义或作用是使得学习器具有了泛化的能力。

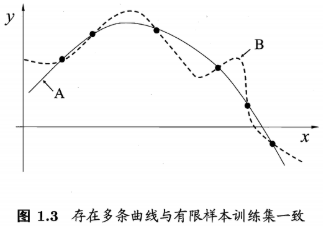
对于上图中的 6 个离散实心点，可由很多不同的曲线拟合之。但训练的模型必然存在一定的 “偏好” 或者说 “倾向”，才能学习出模型自己认为正确的拟合规则。

显然，加了一定正则的偏置的实线 A 比虚线 B 更为简单而通用 (模型复杂度受到惩罚而更低，恰当拟合数据点，泛化性能更好)。

决策树

什么是决策树？

决策树是一种解决分类问题的算法，想要了解分类问题和回归问题，可以看这里《监督学习的2个任务：回归、分类》。

决策树算法采用树形结构，使用层层推理来实现最终的分类。决策树由下面几种元素构成：

根节点：包含样本的全集
内部节点：对应特征属性测试
叶节点：代表决策的结果

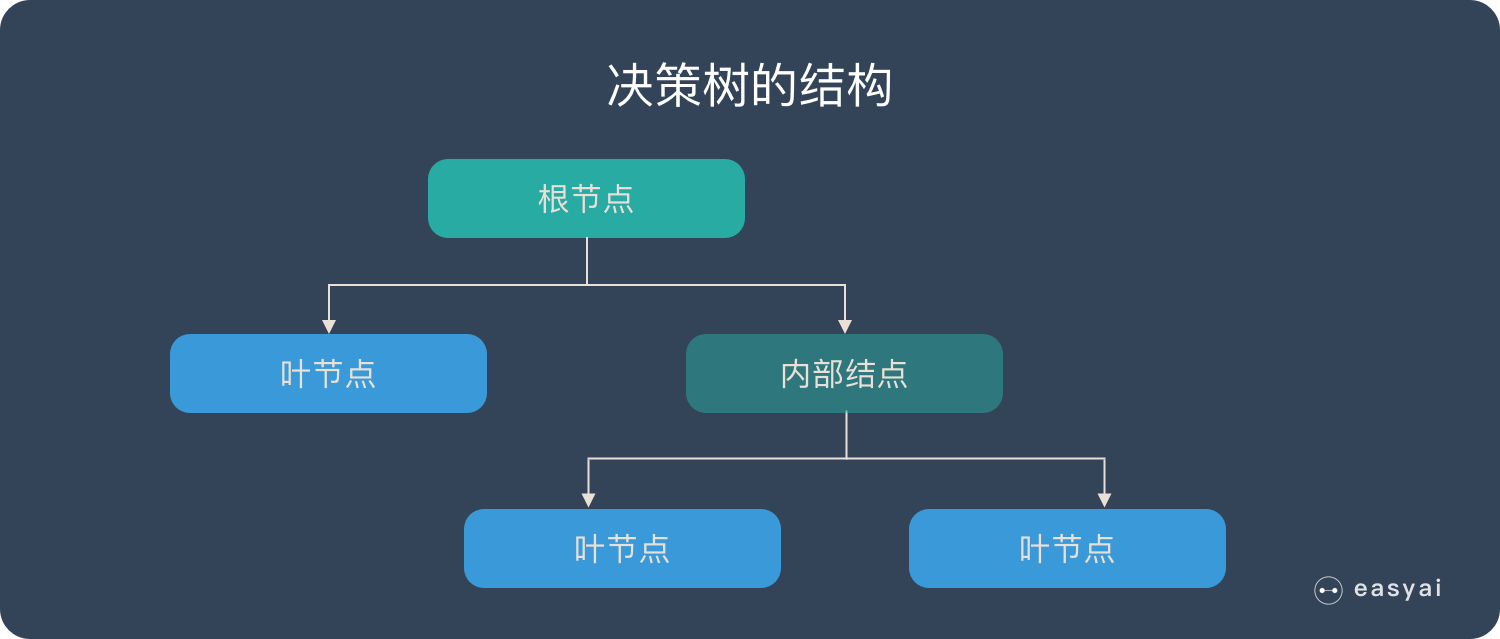
预测时，在树的内部节点处用某一属性值进行判断，根据判断结果决定进入哪个分支节点，直到到达叶节点处，得到分类结果。

这是一种基于 if-then-else 规则的有监督学习算法，决策树的这些规则通过训练得到，而不是人工制定的。

决策树是最简单的机器学习算法，它易于实现，可解释性强，完全符合人类的直观思维，有着广泛的应用。

举个栗子：

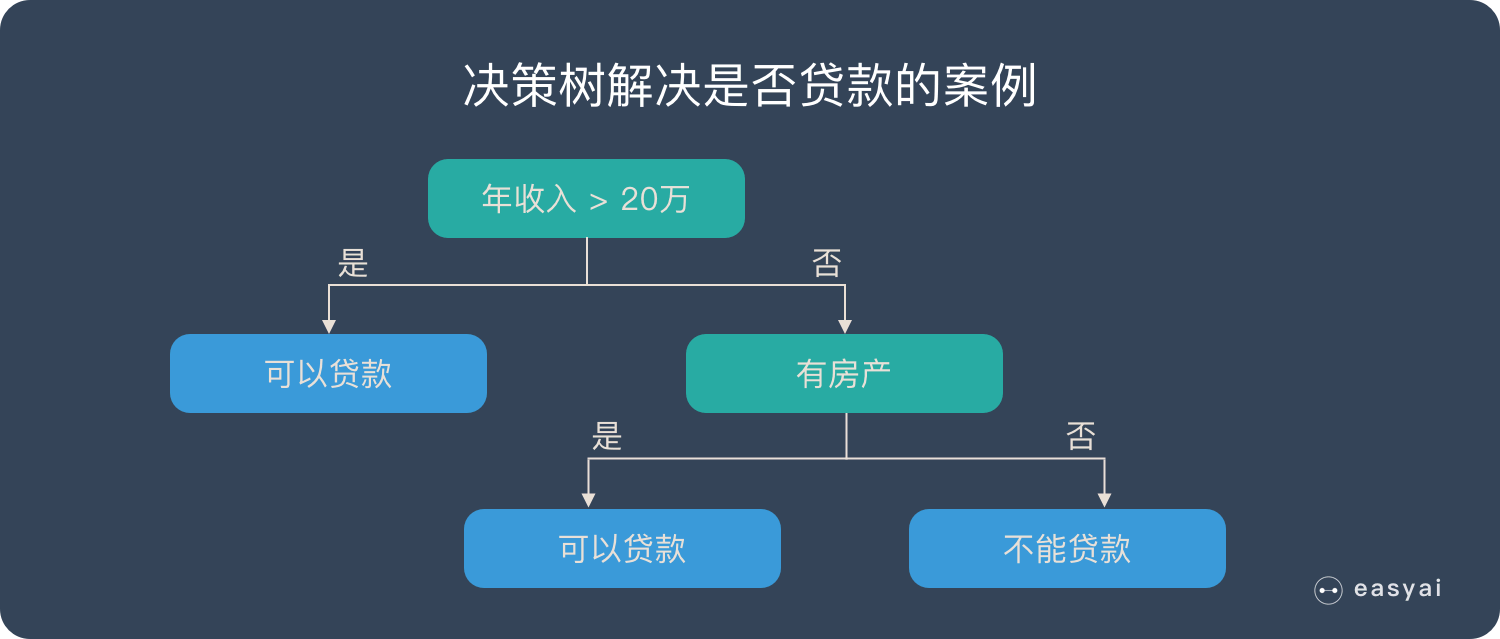
上面的说法过于抽象，下面来看一个实际的例子。银行要用机器学习算法来确定是否给客户发放贷款，为此需要考察客户的年收入，是否有房产这两个指标。领导安排你实现这个算法，你想到了最简单的线性模型，很快就完成了这个任务。

首先判断客户的年收入指标。如果大于20万，可以贷款；否则继续判断。然后判断客户是否有房产。如果有房产，可以贷款；否则不能贷款。

这个例子的决策树如下图所示：

决策树学习与构造

目标：根据给定的训练数据集构建一个决策树模型，使它能够对实例进行正确的分类。决策树学习本质上是从训练数据集中归纳出一组分类规则。能对训练数据进行正确分类的决策树可能有多个，可能没有。在选择决策树时，应选择一个与训练数据矛盾较小的决策树，同时具有很好的泛化能力；而且选择的条件概率模型应该不仅对训练数据有很好的拟合，而且对未知数据有很好的预测。

损失函数：通常是正则化的极大似然函数

策略：是以损失函数为目标函数的最小化

因为从所有可能的决策树中选取最优决策树是NP完全问题，所以现实中决策树学习通常采用启发式方法，近似求解这一最优化问题，得到的决策树是次最优(sub-optimal)的。

决策树学习的算法通常是一个递归地选择最优特征，并根据该特征对训练数据进行分割，使得对各个子数据集有一个最好的分类的过程。包含特征选择、决策树的生成和决策树的剪枝过程。

剪枝：

目的：将树变得更简单，从而使它具有更好的泛化能力。

步骤：去掉过于细分的叶结点，使其回退到父结点，甚至更高的结点，然后将父结点或更高的结点改为新的叶结点。

决策树的生成对应模型的局部选择，决策树的剪枝对应于模型的全局选择。决策树的生成只考虑局部最优，决策树的剪枝则考虑全局最优，通过这种方法减少过拟合。

以下引自 https://zhuanlan.zhihu.com/p/126294494

构造方法

决策树构造的输入是一组带有类别标记的例子，构造的结果是一棵二叉树或多叉树。二叉树的内部节点(非叶子节点)一般表示为一个逻辑判断，如形式为 $a=a_j$ 的逻辑判断，其中 $a$ 代表属性， $a_j$ 是该属性的所有取值：树的边是逻辑判断的分支结果。多叉树(ID3)的内部结点是属性，边是该属性的所有取值，有几个属性值就有几条边。树的叶子节点都是类别标记。

由于数据表示不当、有噪声或者由于决策树生成时产生重复的子树等原因，都会造成产生的决策树过大。因此，简化决策树是一个不可缺少的环节。寻找一棵最优决策树，主要应解决以下3个最优化问题：

生成最少数目的叶子节点；
生成的每个叶子节点的深度最小；
生成的决策树叶子节点最少且每个叶子节点的深度最小。

基本算法

ID3决策树

ID3算法是决策树的一种，它是基于奥卡姆剃刀原理的，即用尽量用较少的东西做更多的事。ID3算法，即Iterative Dichotomiser 3，迭代二叉树3代，是Ross Quinlan发明的一种决策树算法，这个算法的基础就是上面提到的奥卡姆剃刀原理，越是小型的决策树越优于大的决策树，尽管如此，也不总是生成最小的树型结构，而是一个启发式算法。

在信息论中，期望信息越小，那么信息增益就越大，从而纯度就越高。ID3算法的核心思想就是以信息增益来度量属性的选择，选择分裂后信息增益最大的属性进行分裂。该算法采用自顶向下的贪婪搜搜索历可能的决策空间。

信息熵

熵（entropy）表示随机变量不确定性的度量，也就是熵越大，变量的不确定性就越大。设X是一个有限值的离散随机变量，其概率分布为： $P(X=x_i)=p_i,i=1,2,…,n$ 则随机变量 $X$ 的熵定义为： $H(X)=−∑_{i=1}^nlog_2p_i$ ( 若 $p_i=0$ ,定义 $0log0=0$ )

条件熵

条件熵 $H(Y|X)$ 表示在已知随机变量 $X$ 条件下随机变量 $Y$ 的不确定性。随机变量 $X$ 给定的条件下随机变量Y的条件熵为： $H(Y|X)=∑_{i=1}^np_iH(Y|X=x_i),p_i=P(X=x_i)$

信息增益

特征 $A$ 对训练数据集 $D$ 的信息增益 $G(D,A)$ ,定义为集合 $D$ 的经验熵 $H(D)$ 与特征 $A$ 给定条件下 $D$ 的经验条件熵 $H(D|A)$ 之差，即： $G(D,A)=H(D)−H(D|A)$

信息增益大的特征具有更强的分类能力

总结

给定训练数据集 $D$ 和特征 $A$ ：

经验熵 $H(D)$ 表示对数据集 $D$ 进行分类的不确定性

经验条件熵 $H(D|A)$ 表示在特征 $A$ 给定的条件下对数据集 $D$ 进行分类的不确定性

$G(D,A)=H(D)−H(D|A)$ 表示由于特征 $A$ 而使得对数据 $D$ 的分类的不确定性减少的程度。

决策树进行分类的步骤

利用样本数据集构造一颗决策树，并通过构造的决策树建立相应的分类模型。这个过程实际上是从一个数据中获取知识，进行规制提炼的过程。
利用已经建立完成的决策树模型对数据集进行分类。即对未知的数据集元组从根节点依次进行决策树的游历，通过一定的路径游历至某叶子节点，从而找到该数据元组所在的类或类的分布。

ID3决策树示例

示例代码没有剪枝（编者注

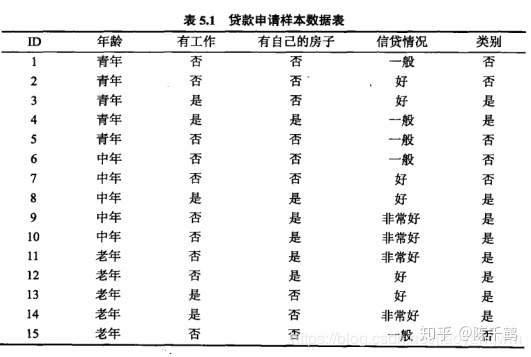
在编写代码之前，我们先对数据集进行属性标注。

年龄：0代表青年，1代表中年，2代表老年；
有工作：0代表否，1代表是；
有自己的房子：0代表否，1代表是；
信贷情况：0代表一般，1代表好，2代表非常好；
类别(是否给贷款)：no代表否，yes代表是。

数据集

dataSet=[[0, 0, 0, 0, 'no'],
            [0, 0, 0, 1, 'no'],
            [0, 1, 0, 1, 'yes'],
            [0, 1, 1, 0, 'yes'],
            [0, 0, 0, 0, 'no'],
            [1, 0, 0, 0, 'no'],
            [1, 0, 0, 1, 'no'],
            [1, 1, 1, 1, 'yes'],
            [1, 0, 1, 2, 'yes'],
            [1, 0, 1, 2, 'yes'],
            [2, 0, 1, 2, 'yes'],
            [2, 0, 1, 1, 'yes'],
            [2, 1, 0, 1, 'yes'],
            [2, 1, 0, 2, 'yes'],
            [2, 0, 0, 0, 'no']]
    labels=['年龄','有工作','有自己的房子','信贷情况']

计算经验熵（香农熵）

$P(X=x_i)=p_i,i=1,2,…,n$

$H(X)=−∑_{i=1}^nlog_2p_i(若pi=0,定义0log0=0)$

from math import log 
def calcShannonEnt(dataSet):
     # 统计数据数量
     numEntries = len(dataSet)
     # 存储每个label出现次数
     label_counts = {}
     # 统计label出现次数
     for featVec in dataSet:
         current_label = featVec[-1]
         if current_label not in label_counts:  # 提取label信息
             label_counts[current_label] = 0  # 如果label未在dict中则加入
         label_counts[current_label] += 1  # label计数
shannon_ent = 0  # 经验熵
# 计算经验熵
for key in label_counts:
    prob = float(label_counts[key]) / numEntries
    shannon_ent -= prob * log(prob, 2)
return shannon_ent

# 运行结果
# 0.9709505944546686

计算信息增益

$G(D,A)=H(D)−H(D|A)$

def splitDataSet(data_set, axis, value):
    ret_dataset = []
    for feat_vec in data_set:
        if feat_vec[axis] == value:
            reduced_feat_vec = feat_vec[:axis]
            reduced_feat_vec.extend(feat_vec[axis + 1:])
            ret_dataset.append(reduced_feat_vec)
    return ret_dataset


def chooseBestFeatureToSplit(dataSet):
    # 特征数量
    num_features = len(dataSet[0]) - 1
    # 计算数据香农熵
    base_entropy = calcShannonEnt(dataSet)
    # 信息增益
    best_info_gain = 0.0
    # 最优特征索引值
    best_feature = -1
    # 遍历所有特征
    for i in range(num_features):
        # 获取dataset第i个特征
        feat_list = [exampel[i] for exampel in dataSet]
        # 创建set集合，元素不可重合
        unique_val = set(feat_list)
        # 经验条件熵
        new_entropy = 0.0
        # 计算信息增益
        for value in unique_val:
            # sub_dataset划分后的子集
            sub_dataset = splitDataSet(dataSet, i, value)
            # 计算子集的概率
            prob = len(sub_dataset) / float(len(dataSet))
            # 计算经验条件熵
            new_entropy += prob * calcShannonEnt(sub_dataset)
        # 信息增益
        info_gain = base_entropy - new_entropy
        # 打印每个特征的信息增益
        print("第%d个特征的信息增益为%.3f" % (i, info_gain))
        # 计算信息增益
        if info_gain > best_info_gain:
            # 更新信息增益
            best_info_gain = info_gain
            # 记录信息增益最大的特征的索引值
            best_feature = i
    print("最优索引值：" + str(best_feature))
    print()
    return best_feature
# 运行结果
# 第0个特征的信息增益为0.083
# 第1个特征的信息增益为0.324
# 第2个特征的信息增益为0.420
# 第3个特征的信息增益为0.363
# 最优索引值：2

树的生成

import operator
def majority_cnt(class_list):
    class_count = {}
    # 统计class_list中每个元素出现的次数
    for vote in class_list:
        if vote not in class_count:
            class_count[vote] = 0
            class_count[vote] += 1
        # 根据字典的值降序排列
        sorted_class_count = sorted(class_count.items(), key=operator.itemgetter(1), reverse=True)
    return sorted_class_count[0][0]


def creat_tree(dataSet, labels, featLabels):
    # 取分类标签(是否放贷：yes or no)
    class_list = [exampel[-1] for exampel in dataSet]
    # 如果类别完全相同则停止分类
    if class_list.count(class_list[0]) == len(class_list):
        return class_list[0]
    # 遍历完所有特征时返回出现次数最多的类标签
    if len(dataSet[0]) == 1:
        return majority_cnt(class_list)
    # 选择最优特征
    best_feature = chooseBestFeatureToSplit(dataSet)
    # 最优特征的标签
    best_feature_label = labels[best_feature]
    featLabels.append(best_feature_label)
    # 根据最优特征的标签生成树
    my_tree = {best_feature_label: {}}
    # 删除已使用标签
    del(labels[best_feature])
    # 得到训练集中所有最优特征的属性值
    feat_value = [exampel[best_feature] for exampel in dataSet]
    # 去掉重复属性值
    unique_vls = set(feat_value)
    for value in unique_vls:
        my_tree[best_feature_label][value] = creat_tree(splitDataSet(dataSet, best_feature, value), labels, featLabels)
    return my_tree
# 运行结果
# {'有自己的房子': {0: {'有工作': {0: 'no', 1: 'yes'}}, 1: 'yes'}}

树的深度和广度计算

def get_num_leaves(my_tree):
    num_leaves = 0
    first_str = next(iter(my_tree))
    second_dict = my_tree[first_str]
    for key in second_dict.keys():
        if type(second_dict[key]).__name__ == 'dict':
            num_leaves += get_num_leaves(second_dict[key])
        else:
                num_leaves += 1
    return num_leaves


def get_tree_depth(my_tree):
    max_depth = 0       # 初始化决策树深度
    firsr_str = next(iter(my_tree))     # python3中myTree.keys()返回的是dict_keys,不在是list,所以不能使用myTree.keys()[0]的方法获取结点属性，可以使用list(myTree.keys())[0]
    second_dict = my_tree[firsr_str]    # 获取下一个字典
    for key in second_dict.keys():
        if type(second_dict[key]).__name__ == 'dict':     # 测试该结点是否为字典，如果不是字典，代表此结点为叶子结点
            this_depth = 1 + get_tree_depth(second_dict[key])
        else:
            this_depth = 1
        if this_depth > max_depth:
            max_depth = this_depth      # 更新层数
    return max_depth
# 运行结果
# 2
# 3

未知数据的预测

def classify(input_tree, feat_labels, test_vec):
    # 获取决策树节点
    first_str = next(iter(input_tree))
    # 下一个字典
    second_dict = input_tree[first_str]
    feat_index = feat_labels.index(first_str)

    for key in second_dict.keys():
        if test_vec[feat_index] == key:
            if type(second_dict[key]).__name__ == 'dict':
                class_label = classify(second_dict[key], feat_labels, test_vec)
            else:
                class_label = second_dict[key]
    return class_label
# 测试
testVec = [0, 1, 1, 1]
    result = classify(myTree, featLabels, testVec)

    if result == 'yes':
        print('放贷')
    if result == 'no':
        print('不放贷')
# 运行结果
# 放贷

树的存储与读取（以二进制形式存储）

import pickle
def storeTree(input_tree, filename):
    # 存储树
    with open(filename, 'wb') as fw:
        pickle.dump(input_tree, fw)


def grabTree(filename):
    # 读取树
    fr = open(filename, 'rb')
    return pickle.load(fr)

完整代码

from math import log
import operator
import pickle


def calcShannonEnt(dataSet):
    # 统计数据数量
    numEntries = len(dataSet)
    # 存储每个label出现次数
    label_counts = {}
    # 统计label出现次数
    for featVec in dataSet:
        current_label = featVec[-1]
        if current_label not in label_counts:  # 提取label信息
            label_counts[current_label] = 0  # 如果label未在dict中则加入
        label_counts[current_label] += 1  # label计数

    shannon_ent = 0  # 经验熵
    # 计算经验熵
    for key in label_counts:
        prob = float(label_counts[key]) / numEntries
        shannon_ent -= prob * log(prob, 2)
    return shannon_ent


def splitDataSet(data_set, axis, value):
    ret_dataset = []
    for feat_vec in data_set:
        if feat_vec[axis] == value:
            reduced_feat_vec = feat_vec[:axis]
            reduced_feat_vec.extend(feat_vec[axis + 1:])
            ret_dataset.append(reduced_feat_vec)
    return ret_dataset


def chooseBestFeatureToSplit(dataSet):
    # 特征数量
    num_features = len(dataSet[0]) - 1
    # 计算数据香农熵
    base_entropy = calcShannonEnt(dataSet)
    # 信息增益
    best_info_gain = 0.0
    # 最优特征索引值
    best_feature = -1
    # 遍历所有特征
    for i in range(num_features):
        # 获取dataset第i个特征
        feat_list = [exampel[i] for exampel in dataSet]
        # 创建set集合，元素不可重合
        unique_val = set(feat_list)
        # 经验条件熵
        new_entropy = 0.0
        # 计算信息增益
        for value in unique_val:
            # sub_dataset划分后的子集
            sub_dataset = splitDataSet(dataSet, i, value)
            # 计算子集的概率
            prob = len(sub_dataset) / float(len(dataSet))
            # 计算经验条件熵
            new_entropy += prob * calcShannonEnt(sub_dataset)
        # 信息增益
        info_gain = base_entropy - new_entropy
        # 打印每个特征的信息增益
        print("第%d个特征的信息增益为%.3f" % (i, info_gain))
        # 计算信息增益
        if info_gain > best_info_gain:
            # 更新信息增益
            best_info_gain = info_gain
            # 记录信息增益最大的特征的索引值
            best_feature = i
    print("最优索引值：" + str(best_feature))
    print()
    return best_feature


def majority_cnt(class_list):
    class_count = {}
    # 统计class_list中每个元素出现的次数
    for vote in class_list:
        if vote not in class_count:
            class_count[vote] = 0
            class_count[vote] += 1
        # 根据字典的值降序排列
        sorted_class_count = sorted(class_count.items(), key=operator.itemgetter(1), reverse=True)
    return sorted_class_count[0][0]


def creat_tree(dataSet, labels, featLabels):
    # 取分类标签(是否放贷：yes or no)
    class_list = [exampel[-1] for exampel in dataSet]
    # 如果类别完全相同则停止分类
    if class_list.count(class_list[0]) == len(class_list):
        return class_list[0]
    # 遍历完所有特征时返回出现次数最多的类标签
    if len(dataSet[0]) == 1:
        return majority_cnt(class_list)
    # 选择最优特征
    best_feature = chooseBestFeatureToSplit(dataSet)
    # 最优特征的标签
    best_feature_label = labels[best_feature]
    featLabels.append(best_feature_label)
    # 根据最优特征的标签生成树
    my_tree = {best_feature_label: {}}
    # 删除已使用标签
    del(labels[best_feature])
    # 得到训练集中所有最优特征的属性值
    feat_value = [exampel[best_feature] for exampel in dataSet]
    # 去掉重复属性值
    unique_vls = set(feat_value)
    for value in unique_vls:
        my_tree[best_feature_label][value] = creat_tree(splitDataSet(dataSet, best_feature, value), labels, featLabels)
    return my_tree


def get_num_leaves(my_tree):
    num_leaves = 0
    first_str = next(iter(my_tree))
    second_dict = my_tree[first_str]
    for key in second_dict.keys():
        if type(second_dict[key]).__name__ == 'dict':
            num_leaves += get_num_leaves(second_dict[key])
        else:
                num_leaves += 1
    return num_leaves


def get_tree_depth(my_tree):
    max_depth = 0       # 初始化决策树深度
    firsr_str = next(iter(my_tree))     # python3中myTree.keys()返回的是dict_keys,不在是list,所以不能使用myTree.keys()[0]的方法获取结点属性，可以使用list(myTree.keys())[0]
    second_dict = my_tree[firsr_str]    # 获取下一个字典
    for key in second_dict.keys():
        if type(second_dict[key]).__name__ == 'dict':     # 测试该结点是否为字典，如果不是字典，代表此结点为叶子结点
            this_depth = 1 + get_tree_depth(second_dict[key])
        else:
            this_depth = 1
        if this_depth > max_depth:
            max_depth = this_depth      # 更新层数
    return max_depth


def classify(input_tree, feat_labels, test_vec):
    # 获取决策树节点
    first_str = next(iter(input_tree))
    # 下一个字典
    second_dict = input_tree[first_str]
    feat_index = feat_labels.index(first_str)

    for key in second_dict.keys():
        if test_vec[feat_index] == key:
            if type(second_dict[key]).__name__ == 'dict':
                class_label = classify(second_dict[key], feat_labels, test_vec)
            else:
                class_label = second_dict[key]
    return class_label


def storeTree(input_tree, filename):
    # 存储树
    with open(filename, 'wb') as fw:
        pickle.dump(input_tree, fw)


def grabTree(filename):
    # 读取树
    fr = open(filename, 'rb')
    return pickle.load(fr)


if __name__ == "__main__":
    # 数据集
    dataSet = [[0, 0, 0, 0, 'no'],
               [0, 0, 0, 1, 'no'],
               [0, 1, 0, 1, 'yes'],
               [0, 1, 1, 0, 'yes'],
               [0, 0, 0, 0, 'no'],
               [1, 0, 0, 0, 'no'],
              # [1, 0, 0, 0, 'yes'],
               [1, 0, 0, 1, 'no'],
               [1, 1, 1, 1, 'yes'],
               [1, 0, 1, 2, 'yes'],
               [1, 0, 1, 2, 'yes'],
               [2, 0, 1, 2, 'yes'],
               [2, 0, 1, 1, 'yes'],
               [2, 1, 0, 1, 'yes'],
               [2, 1, 0, 2, 'yes'],
               [2, 0, 0, 0, 'no']]
    # 分类属性
    labels = ['年龄', '有工作', '有自己的房子', '信贷情况']

    print(dataSet)
    print()
    print(calcShannonEnt(dataSet))
    print()

    featLabels = []
    myTree = creat_tree(dataSet, labels, featLabels)
    print(myTree)
    print(get_tree_depth(myTree))
    print(get_num_leaves(myTree))

    #测试数据
    testVec = [0, 1, 1, 1]
    result = classify(myTree, featLabels, testVec)

    if result == 'yes':
        print('放贷')
    if result == 'no':
        print('不放贷')

    # 存储树
    storeTree(myTree,'classifierStorage.txt')

    # 读取树
    myTree2 = grabTree('classifierStorage.txt')
    print(myTree2)

    testVec2 = [1, 0]
    result2 = classify(myTree2, featLabels, testVec)
    if result2 == 'yes':
        print('放贷')
    if result2 == 'no':
        print('不放贷')
# 运行结果
# [[0, 0, 0, 0, 'no'], [0, 0, 0, 1, 'no'], [0, 1, 0, 1, 'yes'], [0, 1, 1, 0, 'yes'], [0, 0, 0, 0, 'no'], [1, 0, 0, 0, 'no'], [1, 0, 0, 1, 'no'], [1, 1, 1, 1, 'yes'], [1, 0, 1, 2, 'yes'], [1, 0, 1, 2, 'yes'], [2, 0, 1, 2, 'yes'], [2, 0, 1, 1, 'yes'], [2, 1, 0, 1, 'yes'], [2, 1, 0, 2, 'yes'], [2, 0, 0, 0, 'no']]

# 0.9709505944546686

# 第0个特征的信息增益为0.083
# 第1个特征的信息增益为0.324
# 第2个特征的信息增益为0.420
#　第3个特征的信息增益为0.363
# 最优索引值：2

# 第0个特征的信息增益为0.252
# 第1个特征的信息增益为0.918
# 第2个特征的信息增益为0.474
# 最优索引值：1

# {'有自己的房子': {0: {'有工作': {0: 'no', 1: 'yes'}}, 1: 'yes'}}
# 2
# 3
# 放贷
# {'有自己的房子': {0: {'有工作': {0: 'no', 1: 'yes'}}, 1: 'yes'}}
# 放贷

C4.5决策树

C4.5决策树实在ID3决策树的基础上进行了优化。将节点的划分标准替换为了信息增益率，能够处理连续值，并且可以处理缺失值，以及能够进行剪枝操作。

信息增益

信息增益率使用“分裂信息”值将信息增益规范化。分类信息类似于Info(D)，定义如下： $SplitInfoA(D)=−∑_{j=1}^v\dfrac{|Dj|}{|D|}\times log_2(\dfrac{|Dj|}{|D|})$

这个值表示通过将训练数据集D划分成对应于属性A测试的v个输出的v个划分产生的信息。信息增益率定义： $GainRatio(A)=\dfrac{Gain(A)}{SplitInfo(a)}$

此处的 $Gain(A)$ 即是前文介绍ID3时的 $G(D,A)$

选择具有最大增益率的属性作为分裂属性。

当属性有很多值时，虽然信息增益变大了，但是相应的属性熵也会变大。所以最终计算的信息增益率并不是很大。在一定程度上可以避免ID3倾向于选择取值较多的属性作为节点的问题。

具体树的构造方法与前文的ID3相同，这里不再赘述

CART决策树

CART 树（分类回归树）分为分类树和回归树。顾名思义，分类树用于处理分类问题；回归树用来处理回归问题。我们知道分类和回归是机器学习领域两个重要的方向。分类问题输出特征向量对应的分类结果，回归问题输出特征向量对应的预测值。

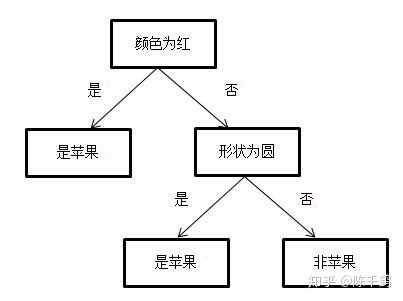
分类树和 ID3、C4.5 决策树相似，都用来处理分类问题。不同之处是划分方法。分类树利用基尼指数进行二分。如图所示就是一个分类树。

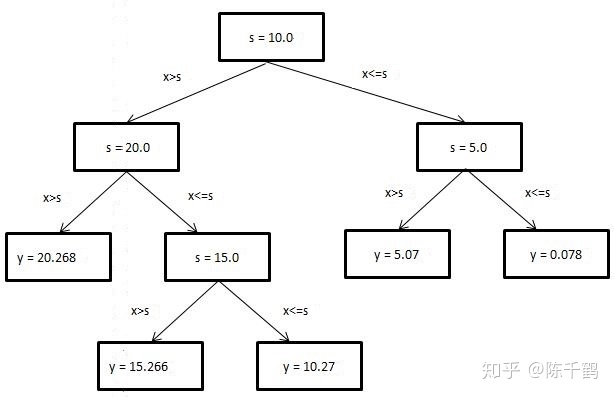
回归树用来处理回归问题。回归将已知数据进行拟合，对于目标变量未知的数据可以预测目标变量的值。如图所示就是一个回归树，其中 s 是切分点，x 是特征，y 是目标变量。可以看出图 2 利用切分点 s 将特征空间进行划分，y 是在划分单元上的输出值。回归树的关键是如何选择切分点、如何利用切分点划分数据集、如何预测 y 的取值。

基尼指数

数据集D的纯度可以用基尼值来度量： $Gini(D)=∑_{k=1}^{|y|}∑_{k′≠k}p_kp_{k′}=1−∑_{k=1}^{|y|}p_k^2$

直观来说， $Gini(D)$ 反映了从数据集D中随机选取两个样本，其类别标记不一致的概率，因此 $Gini(D)$ 越小，则数据集D的纯度越高。

属性 $a$ 的基尼指数定义为 $Gini\_index(D,a)=∑_{V=1}^V\dfrac{|D_v|}{|D|}Gini(D^v)$ 于是，我们在候选属性集合A中，选择那个使得划分后基尼指数最小的属性作为最优划分属性，即$a=arg min Gini_index(D,a),其中a∈A $

回归树没看懂，也没讲

剪枝

决策树的优缺点

优点

决策树易于理解和解释，可以可视化分析，容易提取出规则；
可以同时处理标称型和数值型数据；
比较适合处理有缺失属性的样本；
能够处理不相关的特征；
测试数据集时，运行速度比较快；
在相对短的时间内能够对大型数据源做出可行且效果良好的结果。

缺点

容易发生过拟合（随机森林可以很大程度上减少过拟合）；
容易忽略数据集中属性的相互关联；
对于那些各类别样本数量不一致的数据，在决策树中，进行属性划分时，不同的判定准则会带来不同的属性选择倾向；信息增益准则对可取数目较多的属性有所偏好（典型代表ID3算法），而增益率准则（CART）则对可取数目较少的属性有所偏好，但CART进行属性划分时候不再简单地直接利用增益率尽心划分，而是采用一种启发式规则）（只要是使用了信息增益，都有这个缺点，如RF）。
ID3算法计算信息增益时结果偏向数值比较多的特征。