卡尔曼滤波:理论与实践 定义与应用场景 卡尔曼滤波(Kalman filter)是一种高效的自回归滤波器,它能在存在诸多不确定性情况的组合信息中估计动态系统的状态。对于这个滤波器,我们几乎可以下这么一个定论:只要是存在不确定信息的动态系统 ,卡尔曼滤波就可以对系统下一步要做什么 做出有根据的推测 。即便有噪声信息干扰,卡尔曼滤波通常也能很好的弄清楚究竟发生了什么,找出现象间不易察觉的相关性。因此卡尔曼滤波非常适合不断变化的系统,它的优点还有内存占用较小(只需保留前一个状态)、速度快,是实时问题和嵌入式系统的理想选择。
样例下的卡尔曼滤波推导 举个栗子:你造了一个可以在树林里四处溜达的小机器人,为了让它实现导航,机器人需要知道自己所处的位置。
也就是说,机器人有一个包含位置信息和速度信息的状态 x ⃗ k \vec x_k x k x ⃗ k = ( p ⃗ , v ⃗ ) \vec x_k=(\vec p,\vec v) x k = ( p , v )
我们的小机器人装有GPS传感器 ,定位精度10米。虽然一般来说这点精度够用了,但我们希望它的定位误差能再小点,毕竟树林里到处都是土坑和陡坡,如果机器人稍稍偏了那么几米,它就有可能滚落山坡。所以GPS提供的信息还不够充分。
我们也可以预测 机器人是怎么移动的:它会把指令发送给控制轮子的马达,如果这一刻它始终朝一个方向前进,没有遇到任何障碍物,那么下一刻它可能会继续坚持这个路线。但是机器人对自己的状态不是全知的:它可能会逆风行驶,轮子打滑,滚落颠簸地形……所以车轮转动次数并不能完全代表实际行驶距离,基于这个距离的预测也不完美。
这个问题下,GPS为我们提供了一些关于状态的信息,但那是间接的、不准确的;我们的预测提供了关于机器人轨迹的信息,但那也是间接的、不准确的。
但以上就是我们能够获得的全部信息,在它们的基础上,我们是否能给出一个完整预测,让它的准确度比机器人搜集的单次预测汇总更高?也就是说,我们希望使用一些低精准度的信息预测一个精准度相对较高的结果。用了卡尔曼滤波,这个问题可以迎刃而解。
卡尔曼滤波眼里的机器人问题 还是上面这个问题,我们有一个状态,它和速度、位置有关:
x ⃗ = [ p v ] \vec x = \left[ \begin{matrix} p \\ v \end{matrix} \right] x = [ p v ]
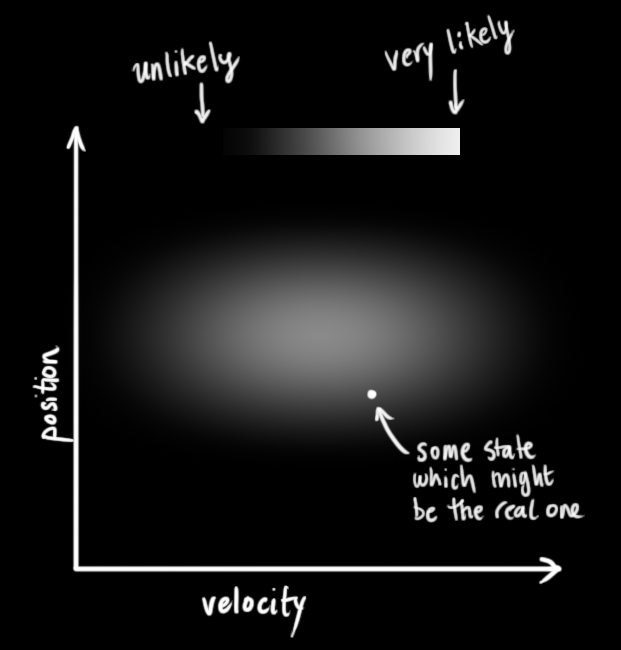
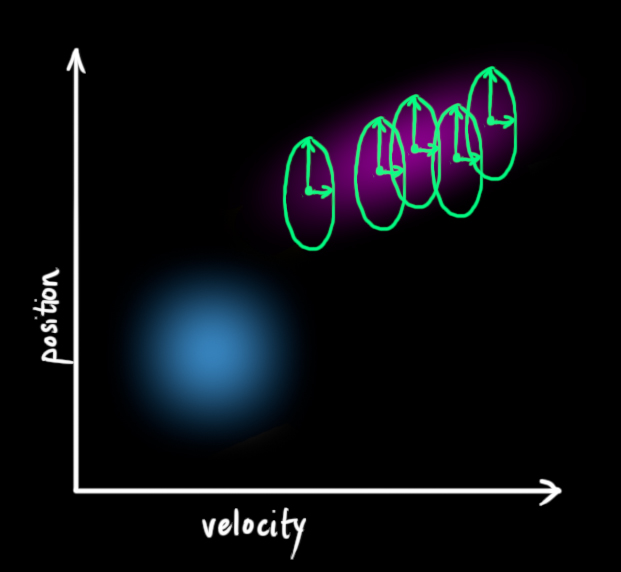
我们不知道它们的实际值是多少,但掌握着一些速度和位置的可能组合 ,其中某些组合的可能性更高:
图中我们画出了状态的二维描述,越趋近于白色的区域是发生概率更大的区域(也就是系统真实状态更可能处于的位置),区域中就可能包含了我们当前系统的实际位置。
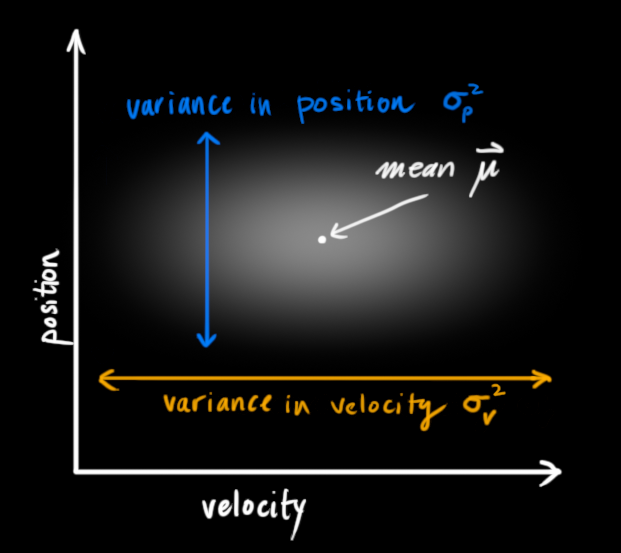
卡尔曼滤波假设两个变量(在我们的例子里是位置和速度)都应该是随机的 ,而且符合高斯分布 。每个变量 都有一个均值 μ μ μ σ 2 σ^2 σ 2 μ ⃗ = ( μ v , μ p ) \vec\mu=(\mu_v,\mu_p) μ = ( μ v , μ p )
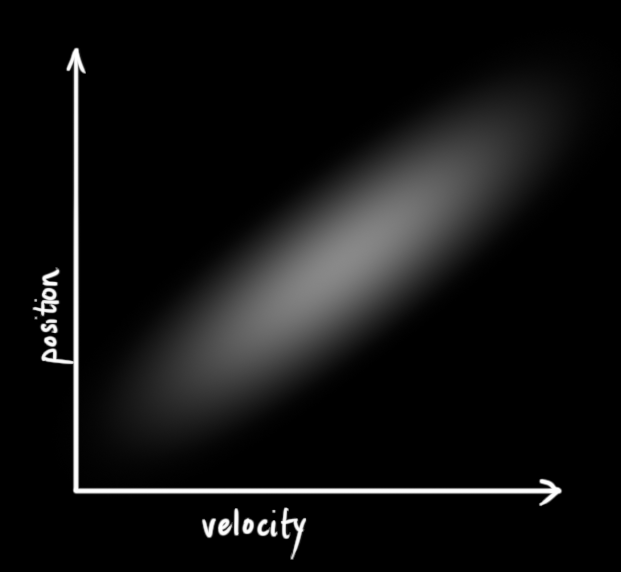
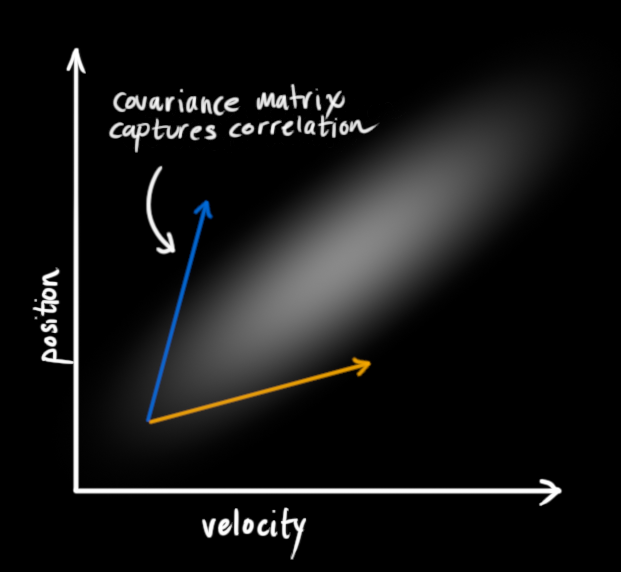
在上图中,位置和速度是不相关 的,所以可能的取值区域呈现出一种类似圆形的图形,这意味着某个变量的状态不会告诉你其他变量的状态是怎样的。即,我们虽然知道现在的速度,但无法从现在的速度推测出现在的位置。但实际上并非如此,我们知道速度和位置是有关系的(correlated ),如下图所示,机器人前往特定位置的可能性取决于它拥有的速度。
这不难理解,如果基于旧位置估计新位置,我们会产生这两个结论:如果速度很快,机器人可能移动得更远,所以得到的位置会更远;如果速度很慢,机器人就走不了那么远。
这种关系对目标跟踪来说非常重要,因为它提供了更多信息:一个可以衡量可能性的标准 。这就是卡尔曼滤波的目标:从不确定信息中挤出尽可能多的信息!
为了捕获这种相关性,我们用的是协方差矩阵 。简而言之,矩阵的每个值是第 i i i j j j 相关程度 (由于矩阵是对称的,i i i j j j Σ Σ Σ Σ i j Σ_{ij} Σ ij
(下文对协方差矩阵给了具体解释)
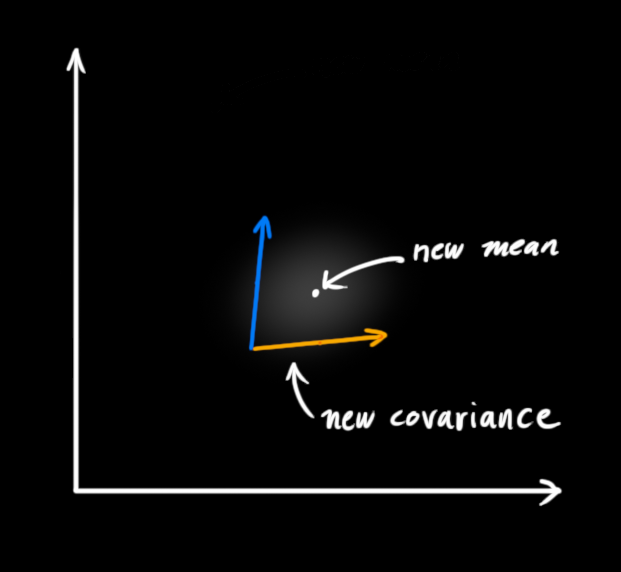
用矩阵描述问题 为了把以上关于状态的信息建模为高斯分布(图中色块),我们还需要 k k k 此时刻系统状态的最佳估计 x ^ k \hat x_k x ^ k μ μ μ 最佳估计的协方差矩阵 P k P_k P k
卡尔曼滤波器需要预设一个对状态的初始猜测值,这个值不用很精准,后面会提到
x ^ k = [ p o s i t i o n v e l o c i t y ] P k = [ ∑ p p ∑ p v ∑ v p ∑ v v ] \hat x_k=\left[ \begin{matrix} position \\ velocity \end{matrix} \right] \\ P_k=\left[ \begin{matrix} \sum _{pp} & \sum _{pv}\\ \sum _{vp} & \sum _{vv} \end{matrix} \right] x ^ k = [ p os i t i o n v e l oc i t y ] P k = [ ∑ pp ∑ v p ∑ p v ∑ vv ]
也即:
P k = [ C o v ( p , p ) C o v ( p , v ) C o v ( v , p ) C o v ( v , v ) ] P_k=\left[ \begin{matrix} Cov(p,p) & Cov(p,v)\\ Cov(v,p) & Cov(v,v) \end{matrix} \right] P k = [ C o v ( p , p ) C o v ( v , p ) C o v ( p , v ) C o v ( v , v ) ]
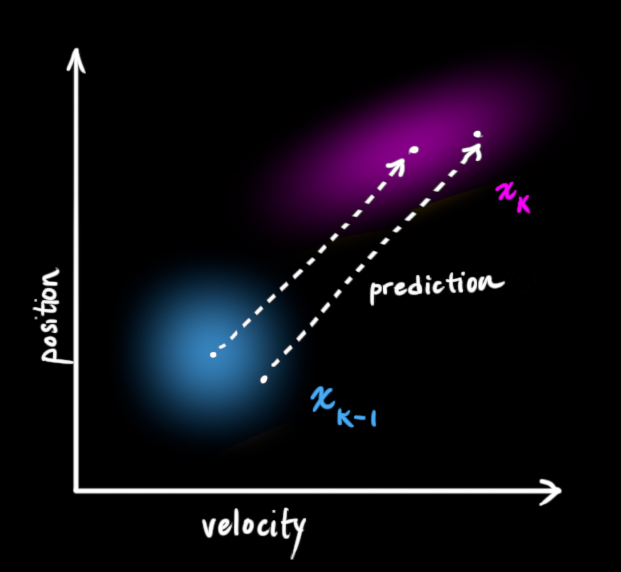
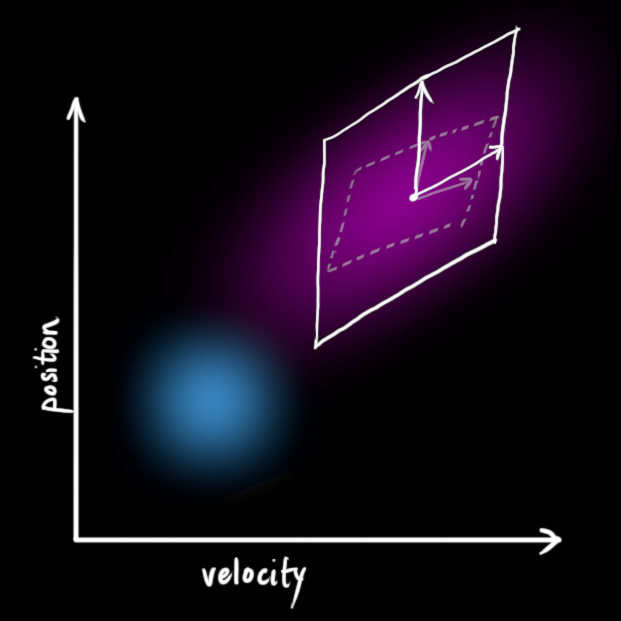
接下来,我们要通过查看当前状态(k − 1 k-1 k − 1 (k k k 预测 (prediction)并不在乎这些:
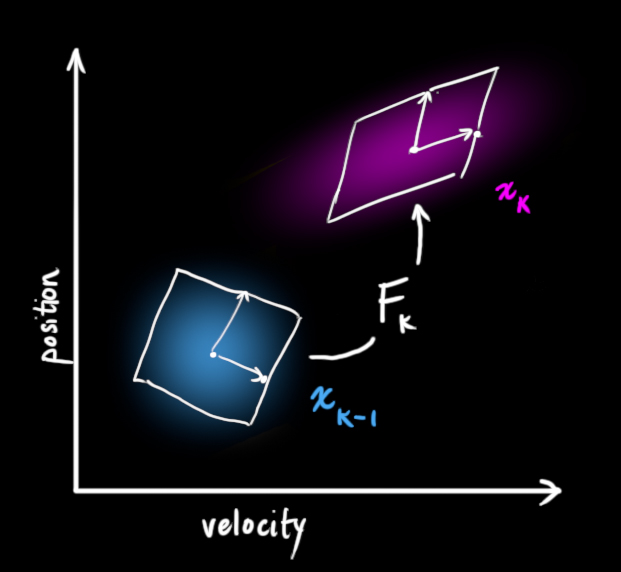
我们可以用状态转移矩阵 F k F_k F k F k F_k F k x k − 1 x_{k-1} x k − 1 x k x_k x k
它从原始预测中取每一点,并将其移动到新的预测位置。如果原始预测是正确的,系统就会移动到新位置。
这是怎么做到的?为什么我们可以用矩阵来预测机器人下一刻的位置和速度?下面是个简单公式:
p k = p k − 1 + Δ t ⋅ v k − 1 v k = v k − 1 \begin{aligned} \color{magenta}p_k&={\color{blue}p_{k-1}}+\Delta t\cdot \color{blue}v_{k-1}\\ \color{magenta}v_k&= \color{blue}v_{k-1} \end{aligned} p k v k = p k − 1 + Δ t ⋅ v k − 1 = v k − 1
换成矩阵形式:
x ^ k = [ 1 Δ t 0 1 ] x ^ k − 1 = F k ⋅ x ^ k − 1 \begin{aligned} \color{magenta}\hat x_k &=\left[ \begin{matrix} \,1&\Delta t\, \\ 0&1 \end{matrix} \right]\color{blue}\hat x_{k-1}\\ &=F_k\cdot \color{blue}\hat x_{k-1} \end{aligned} x ^ k = [ 1 0 Δ t 1 ] x ^ k − 1 = F k ⋅ x ^ k − 1
这是一个预测矩阵,它能给出机器人的下一个状态,但目前我们还不知道协方差矩阵的更新方法。这也是我们要引出下面这个等式的原因:如果我们将分布中的每个点乘以矩阵 A A A
C o v ( x ) = ∑ C o v ( A x ) = A ∑ A T Cov(x)=\textstyle\sum\\ Cov(Ax) = A\textstyle\sum A^T C o v ( x ) = ∑ C o v ( A x ) = A ∑ A T
把这个式子和上面的最佳估计 x ^ k \hat x_k x ^ k
x ^ k = F k ⋅ x ^ k − 1 C o v ( x ^ k ) = C o v ( F k ⋅ x ^ k − 1 ) = F k ⋅ C o v ( x ^ k − 1 ) ⋅ F k T \hat x_k=F_k\cdot \hat x_{k-1}\\ \\ \begin{aligned} Cov(\hat x_k) &= Cov(F_k\cdot \hat x_{k-1})\\ &= F_k\cdot Cov(\hat x_{k-1})\cdot F_k^T \end{aligned}\\ x ^ k = F k ⋅ x ^ k − 1 C o v ( x ^ k ) = C o v ( F k ⋅ x ^ k − 1 ) = F k ⋅ C o v ( x ^ k − 1 ) ⋅ F k T
下式就相当于(注意小写 p p p P P P
P k = F k ⋅ P k − 1 ⋅ F k T {\color{magenta}P_k}=F_k\cdot {\color{blue}P_{k-1}}\cdot F_k^T P k = F k ⋅ P k − 1 ⋅ F k T
因为 P k P_k P k x ^ k \hat x_k x ^ k P k = C o v ( x ^ k ) P_k=Cov(\hat x_k) P k = C o v ( x ^ k )
外部影响 已知的外部控制 但是,除了速度和位置,外因也会对系统造成影响。比如模拟火车运动,除了列车自驾系统,列车操作员可能会手动调速。在我们的机器人示例中,导航软件也可以发出停止指令或者加速指令。对于这些信息,我们把它作为一个向量 u ⃗ k \color{orange}\vec u_k u k
假设油门设置和控制命令是已知的,我们知道火车的预期加速度 a \color{orange}a a
p k = p k − 1 + Δ t v k − 1 + 1 2 a Δ t 2 v k = v k − 1 + a Δ t \begin{aligned} \color{magenta}p_k&={\color{blue}p_{k-1}}+\Delta t {\color{blue}v_{k-1}}+\dfrac 1 2 {\color{orange}a}\Delta t^2\\ \color{magenta}v_k&= \kern1cm\kern1cm\,\, {\color{blue}v_{k-1}}+{\color{orange}a}\Delta t \end{aligned} p k v k = p k − 1 + Δ t v k − 1 + 2 1 a Δ t 2 = v k − 1 + a Δ t
把它转成矩阵形式:
x ^ k = F k x ^ k − 1 + [ 1 2 Δ t 2 Δ t ] a = F k x ^ k − 1 + B k ⋅ u ⃗ k \begin{aligned} \color{magenta}\hat x_k&=F_k {\color{blue}\hat x_{k-1}}+\left[ \begin{matrix} \dfrac1 2\Delta t^2 \\ \Delta t \end{matrix} \right]\,\color{orange}a\\ &= F_k {\color{blue}\hat x_{k-1}}+B_k\cdot \color{orange}\vec u_k \end{aligned} x ^ k = F k x ^ k − 1 + [ 2 1 Δ t 2 Δ t ] a = F k x ^ k − 1 + B k ⋅ u k
B k B_k B k u ⃗ k \vec u_k u k
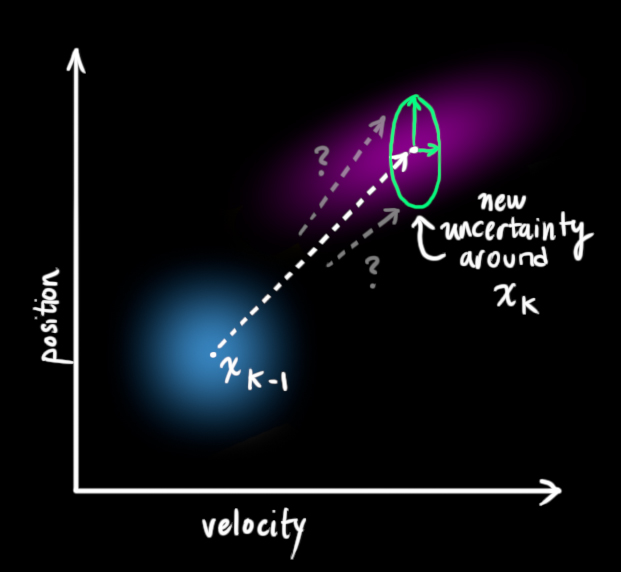
外部不确定性 当我们监控无人机时,它可能会受到风的影响;当我们跟踪轮式机器人时,它的轮胎可能会打滑,或者粗糙地面会降低它的移速。这些因素是难以掌握的,如果出现其中的任意一种情况,预测结果就难以保障。
这要求我们在每个预测步骤后再加上一些新的不确定性,来模拟和“世界”相关的所有不确定性:
如上图所示,加上外部不确定性后, x ^ k − 1 \color{blue}\hat x_{k-1} x ^ k − 1 Q k \color{turquoise}{Q_k} Q k 我们把协方差 Q k \color{turquoise}{Q_k} Q k 。
这个紫色的高斯分布拥有和原分布相同的均值,但协方差不同。造成不同的原因就是噪声的加入,尤其是对于边界的情况,噪声的加入使得紫色范围(新的状态的可能范围)变得比原来更大。
我们在原式上加入 Q k \color{turquoise}Q_k Q k
x ^ k = F k x ^ k − 1 + B k ⋅ u ⃗ k P k = F k ⋅ P k − 1 ⋅ F k T + Q k (7) \begin{aligned} \color{magenta}\hat x_k &= F_k {\color{blue}\hat x_{k-1}}+B_k\cdot \color{orange}\vec u_k\\ \color{magenta}P_k&=F_k\cdot{\color{magenta} P_{k-1}}\cdot F_k^T+\color{turquoise}Q_k \end{aligned}\tag7 x ^ k P k = F k x ^ k − 1 + B k ⋅ u k = F k ⋅ P k − 1 ⋅ F k T + Q k ( 7 )
简而言之,这里:
新的最佳估计(x ^ k \hat x_k x ^ k x ^ k − 1 \hat x_{k-1} x ^ k − 1 u k u_k u k
新的不确定性(P k P_k P k P k − 1 P_{k-1} P k − 1 Q k Q_k Q k
现在,有了这些概念介绍,我们可以把传感器数据输入其中。
通过测量来细化估计值 我们可能有好几个传感器,它们一起提供有关系统状态的信息。传感器的作用不是我们关心的重点,它可以读取位置,可以读取速度,重点是,它能告诉我们关于状态的间接信息——它是状态下产生的一组读数 。
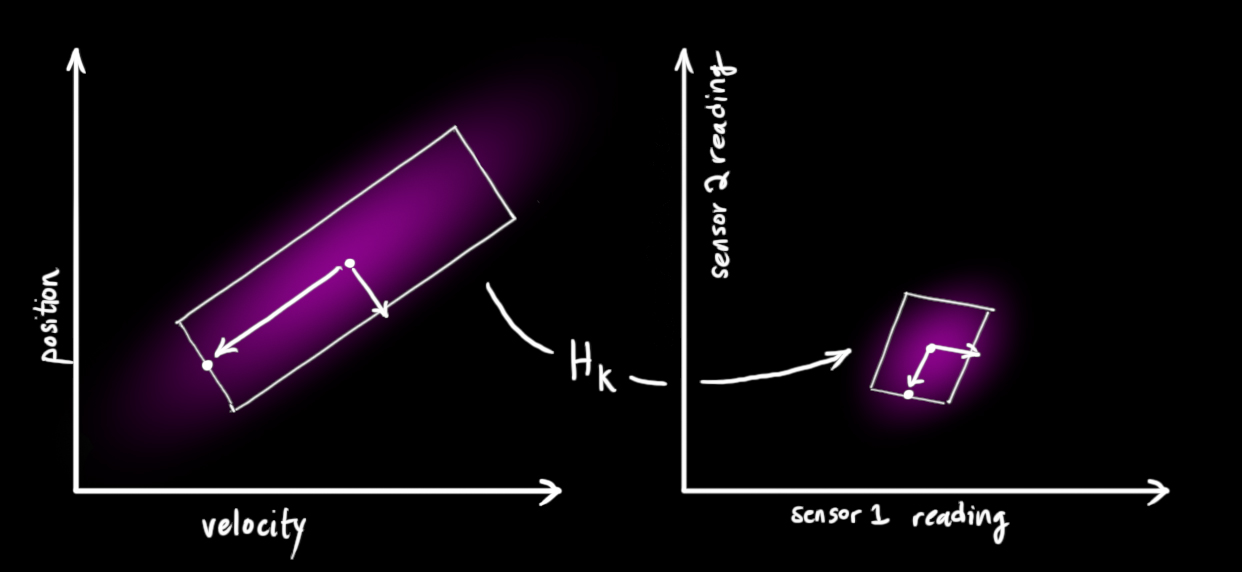
注意,读数的规模和状态的规模不一定相同,所以我们把传感器读数矩阵设为 H k H_k H k
也就是说,真实情况下的位置与速度经过 H k H_k H k H H H
把这些分布转换为一般形式:
μ ⃗ e x p e c t e d = H k ⋅ x ^ k ∑ e x p a n d e d = H k ⋅ P k ⋅ H k T \begin{aligned} \vec \mu_{expected} &= H_k\cdot \color{magenta}\hat x_k\\ \textstyle\sum_{expanded} &=H_k\cdot{\color{magenta}{P_k}}\cdot H_k^T \end{aligned} μ e x p ec t e d ∑ e x p an d e d = H k ⋅ x ^ k = H k ⋅ P k ⋅ H k T
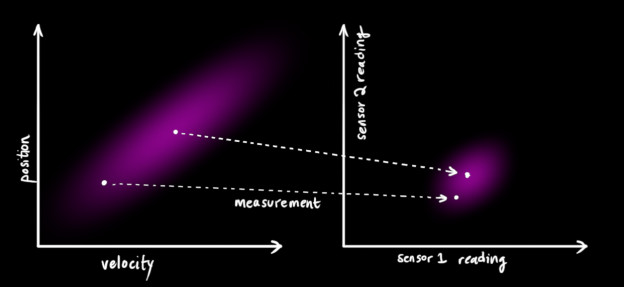
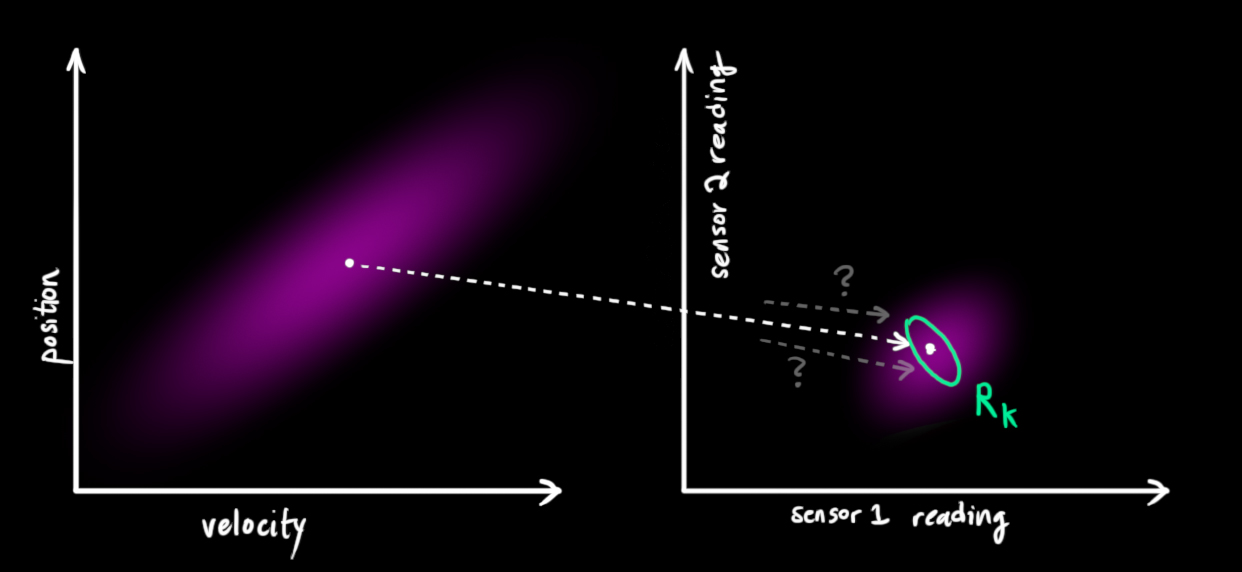
卡尔曼滤波的一大优点是擅长处理传感器噪声 。换句话说,由于种种因素,传感器记录的信息其实是不准的,一个状态事实上可以产生多种读数,就比如车在原地不动,但是由于GPS定位误差可能会给出一段不一样的位置数据。
如下图,左图中一个状态对应右图传感器的多个读数:
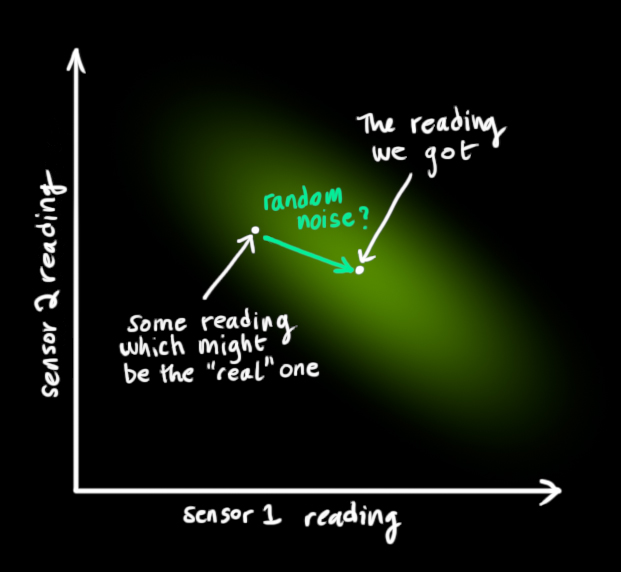
从我们观察到的每一次读数中,我们可能会猜测我们的系统处于特定状态。但由于存在不确定性,一些状态比其他状态更有可能 产生我们所看到的读数:
我们将这种不确定性(即传感器噪声)的协方差设为 R k \color{Emerald}R_k R k z k \color{LimeGreen} z_k z k
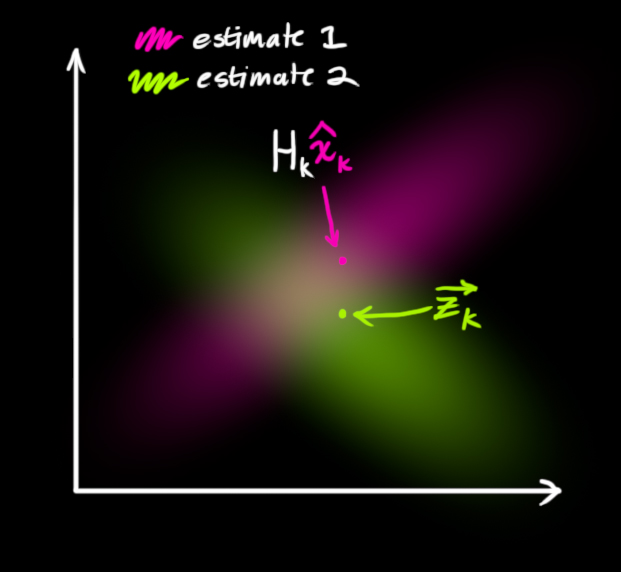
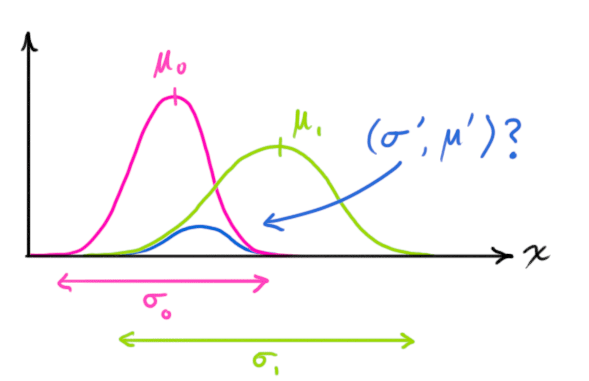
如果要生成靠谱预测,模型必须调和这两个信息(紫色的状态预测与绿色的传感器读数)。也就是说,对于任何可能的读数 ( z 1 , z 2 ) (z_1,z_2) ( z 1 , z 2 )
也就是说,我们现在有两个概率,我们想知道在何种情况下两者都为真,也就是说我们的预测与传感器的读数都反映了真实的状态。最简单的方法是两者相乘:
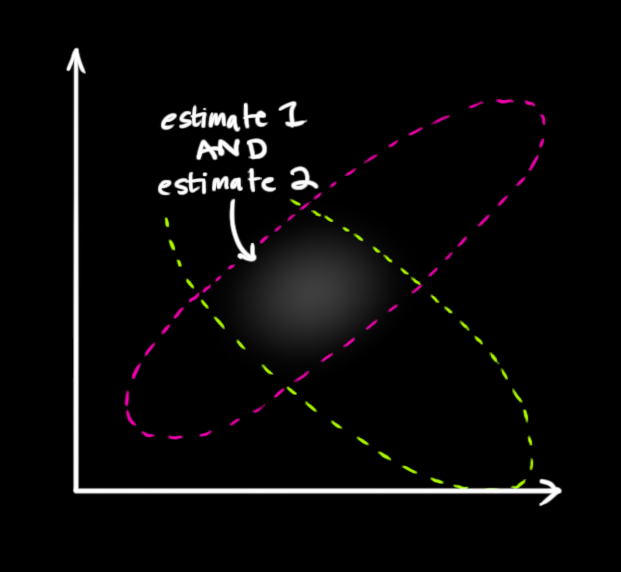
两块高斯分布相乘后,我们可以得到它们的重叠部分(图中白色部分),此分布的均值是两种估计最有可能 的情况,而且它比我们之前的任何一个估计都精确得多,这也是基于我们所有信息的最佳估计的区域。换个角度看,它看起来也符合高斯分布:
事实证明,当你把两个高斯分布和它们各自的均值和协方差矩阵相乘时,你会得到一个拥有独立均值和协方差矩阵的新高斯分布。最后剩下的问题就不难解决了:我们必须有一个公式来从旧的参数中获取这些新参数!
高斯函数 让我们从一维看起,设方差为 σ 2 σ^2 σ 2 μ μ μ
N ( x , μ , σ ) = 1 σ 2 π e − ( x – μ ) 2 2 σ 2 (9) \mathcal{N}(x,μ,σ)=\dfrac 1 {σ\sqrt{2π}}e^{−\dfrac{(x–μ)^2}{2σ^2}}\tag 9 N ( x , μ , σ ) = σ 2 π 1 e − 2 σ 2 ( x – μ ) 2 ( 9 )
那么两条高斯曲线相乘呢?下图中蓝色的曲线就反映了两条高斯曲线(未归一化)的交集。
N ( x , μ 0 , σ 0 ) ⋅ N ( x , μ 1 , σ 1 ) = ? N ( x , μ ′ , σ ′ ) (10) {\color{magenta}\mathcal{N}(x,μ_0,σ_0)}\cdot {\color{LimeGreen}\mathcal{N}(x,μ_1,σ_1)}\overset?={\color{blue}\mathcal{N}(x,μ',σ')}\tag{10} N ( x , μ 0 , σ 0 ) ⋅ N ( x , μ 1 , σ 1 ) = ? N ( x , μ ′ , σ ′ ) ( 10 )
将式 ( 9 ) (9) ( 9 ) ( 10 ) (10) ( 10 )
μ ′ = μ 0 + σ 0 2 ( μ 1 − μ 0 ) σ 0 2 + σ 1 2 σ ′ 2 = σ 0 2 − σ 0 4 σ 0 2 + σ 1 2 (11) \begin{aligned} \mu' &= \mu_0+\dfrac{\sigma_0^2(\mu_1-\mu_0)}{\sigma_0^2+\sigma_1^2}\\ \sigma'^2 &= \sigma_0^2-\dfrac{\sigma_0^4}{\sigma_0^2+\sigma_1^2} \end{aligned}\tag{11} μ ′ σ ′2 = μ 0 + σ 0 2 + σ 1 2 σ 0 2 ( μ 1 − μ 0 ) = σ 0 2 − σ 0 2 + σ 1 2 σ 0 4 ( 11 )
我们用k简化一下:
k = σ 0 2 σ 0 2 + σ 1 2 μ ′ = μ 0 + k ( μ 1 − μ 0 ) σ ′ 2 = σ 0 2 − k σ 0 2 \begin{aligned} {\color{purple}k}&=\dfrac{\sigma_0^2}{\sigma_0^2+\sigma_1^2}\\ \mu' &= \mu_0+{\color{purple}k}\,(\mu_1-\mu_0)\\ \sigma'^2 &= \sigma_0^2-{\color{purple}k}\,\sigma_0^2 \end{aligned} k μ ′ σ ′2 = σ 0 2 + σ 1 2 σ 0 2 = μ 0 + k ( μ 1 − μ 0 ) = σ 0 2 − k σ 0 2
以上是一维的内容,如果是多维空间,把上式转成矩阵格式,其中 ∑ \sum ∑ μ ⃗ \vec\mu μ
K = ∑ 0 ∑ 0 + ∑ 1 (14) {\color{purple}K}=\dfrac{\sum_0}{\sum_0+\sum_1}\tag{14} K = ∑ 0 + ∑ 1 ∑ 0 ( 14 )
μ ⃗ ′ = μ ⃗ 0 + K ( μ ⃗ 1 − μ ⃗ 0 ) ∑ ′ = ∑ 0 − K ∑ 0 (15) \begin{aligned} {\color{skyBlue}\vec\mu'} &= \vec\mu_0+{\color{purple}K}\,(\vec\mu_1-\vec\mu_0)\\ {\color{blue}\textstyle\sum'} &= \textstyle\sum_0-{\color{purple}K}\,\textstyle\sum_0 \end{aligned}\tag{15} μ ′ ∑ ′ = μ 0 + K ( μ 1 − μ 0 ) = ∑ 0 − K ∑ 0 ( 15 )
这个矩阵 K {\color{purple}K} K 卡尔曼增益 ,我们马上就会用上。
结合在一起 截至目前,我们有用矩阵 ( μ 0 , Σ 0 ) = ( H k x ^ k , H k P k H k T ) ({\color{Magenta}μ_0},{\color{Red}Σ_0})=({\color{Magenta}H_k\hat{x}_k},{\color{Red}H_kP_kH_{k}^{T}}) ( μ 0 , Σ 0 ) = ( H k x ^ k , H k P k H k T ) ( μ 1 , Σ 1 ) = ( z ⃗ k , R k ) ({\color{LimeGreen}μ_1},{\color{Turquoise}Σ_1})=({\color{LimeGreen}\vec{z}_k},{\color{Turquoise}R_k}) ( μ 1 , Σ 1 ) = ( z k , R k ) ( μ ⃗ ′ , ∑ ′ ) = ( H k x ^ k ′ , H k P k ′ H k T ) ({\color{skyBlue}\vec\mu'},{\color{CornflowerBlue}\sum'})=(H_k{\color{skyBlue}\hat x_k'},H_k{\color{CornflowerBlue}P_k'}H_k^T) ( μ ′ , ∑ ′ ) = ( H k x ^ k ′ , H k P k ′ H k T )
H k x ^ k ′ = H k x ^ k + K ( z ⃗ k − H k x ^ k ) H k P k ′ H k T = H k P k H k T − K H k P k H k T (16) \begin{aligned} H_k{\color{skyBlue}\hat x_k'} &= {\color{Magenta}H_k\hat{x}_k}&&+{\color{purple}K}({\color{LimeGreen}\vec{z}_k}-{\color{Magenta}H_k\hat{x}_k})\\ H_k{\color{CornflowerBlue}P_k'}H_k^T &= {\color{Red}H_kP_kH_{k}^{T}} &&-{\color{purple}K}{\color{Red}H_kP_kH_{k}^{T}} \end{aligned}\tag{16} H k x ^ k ′ H k P k ′ H k T = H k x ^ k = H k P k H k T + K ( z k − H k x ^ k ) − K H k P k H k T ( 16 )
相应的对于式(14),卡尔曼增益就是:
K = H k P k H k T H k P k H k T + R k (17) {\color{purple}K}=\dfrac{ {\color{Red}H_kP_kH_{k}^{T} } }{ {\color{Red}H_kP_kH_{k}^{T}}+{\color{Turquoise}R_k}}\tag{17} K = H k P k H k T + R k H k P k H k T ( 17 )
考虑到 K 里还包含着一个 H k H_k H k H k H_k H k H k T H_k^T H k T
K ′ = P k H k T H k P k H k T + R k (19) {\color{purple}K'}=\dfrac{ {\color{Red}P_kH_{k}^{T} } } { {\color{Red}H_kP_kH_{k}^{T}}+{\color{Turquoise}R_k} }\tag{19} K ′ = H k P k H k T + R k P k H k T ( 19 )
x ^ k ′ = H k x ^ k + K ′ ( z ⃗ k − H k x ^ k ) P k ′ = H k P k − K ′ H k P k (18) \begin{aligned} {\color{skyBlue}\hat x_k'} &= {\color{Magenta}H_k\hat{x}_k}&&+{\color{purple}K'}({\color{LimeGreen}\vec{z}_k}-{\color{Magenta}H_k\hat{x}_k})\\ {\color{CornflowerBlue}P_k'} &= {\color{Red}H_kP_k} &&-{\color{purple}K'}{\color{Red}H_kP_k} \end{aligned}\tag{18} x ^ k ′ P k ′ = H k x ^ k = H k P k + K ′ ( z k − H k x ^ k ) − K ′ H k P k ( 18 )
最后, x ^ k ′ {\color{skyBlue}\hat x_k'} x ^ k ′ P k ′ {\color{CornflowerBlue}P_k'} P k ′ predict or update :
一个小问题:如何确定初始值? 随机值 很多情况下我们会使用随机数。
卡尔曼滤波对于初始值是很友好的,如果知道初值的大致区间,在这个区间内随机取,基于卡尔曼滤波的强大能力,一般情况下都不会发散的。此时我一般会把P取大一点,虽然初值有偏,但慢慢迭代,没多久系统就会让偏差急剧缩小。
期望 来自https://www.coursera.org/lecture/battery-state-of-charge/3-3-6-how-do-i-initialize-and-tune-a-kalman-filter-6WI1Z
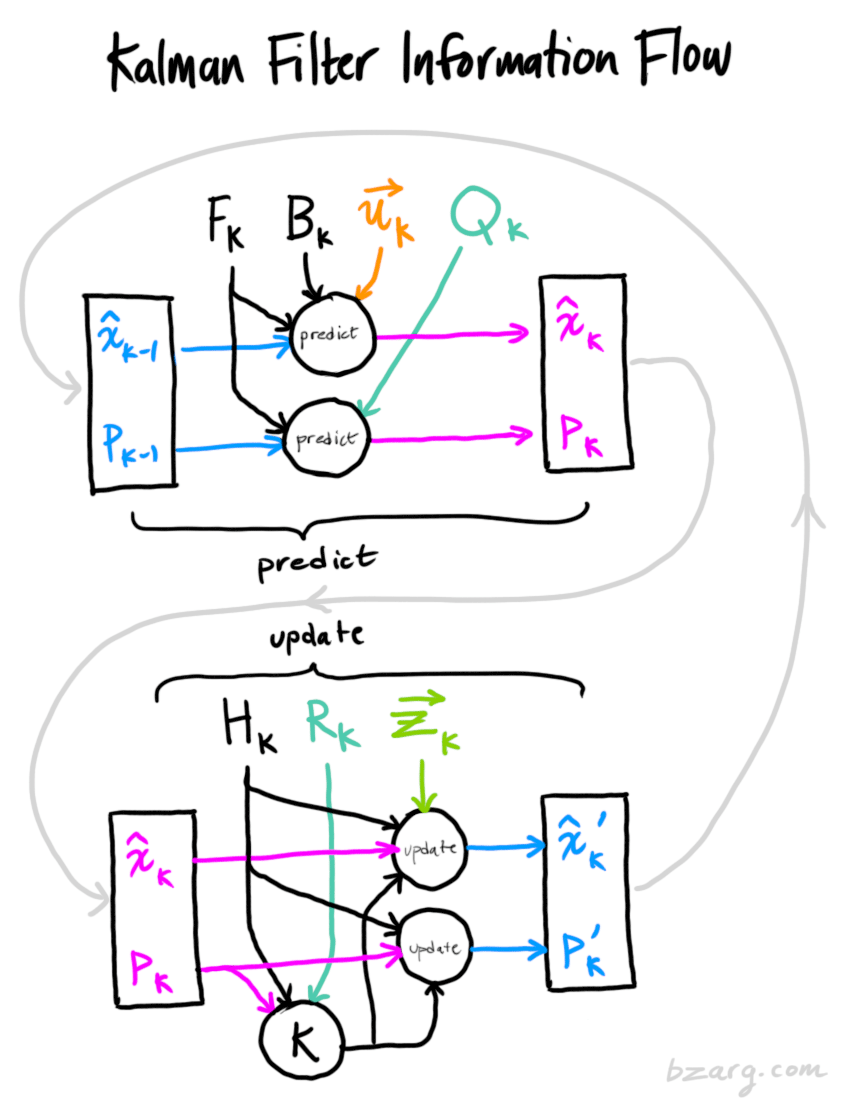
总结 我们主要经历了两个过程:
预测:
更新:
K ′ = P k H k T H k P k H k T + R k (19) {\color{purple}K'}=\dfrac{\color{Red}P_kH_{k}^T}{ {\color{Red}H_kP_kH_{k}^T}+{\color{Turquoise}R_k} }\tag{19} K ′ = H k P k H k T + R k P k H k T ( 19 )
x ^ k ′ = H k x ^ k + K ′ ( z ⃗ k − H k x ^ k ) P k ′ = H k P k − K ′ H k P k (18) \begin{aligned} {\color{skyBlue}\hat x_k'} &= {\color{Magenta}H_k\hat{x}_k}&&+{\color{purple}K'}({\color{LimeGreen}\vec{z}_k}-{\color{Magenta}H_k\hat{x}_k})\\ {\color{CornflowerBlue}P_k'} &= {\color{Red}H_kP_k} &&-{\color{purple}K'}{\color{Red}H_kP_k} \end{aligned}\tag{18} x ^ k ′ P k ′ = H k x ^ k = H k P k + K ′ ( z k − H k x ^ k ) − K ′ H k P k ( 18 )
我们需要调节的参数就是R/Q/P这三个。在正常的卡尔曼滤波中,R和Q不变,我们可以通过噪声的测量来确定这两个值,或者采用最速下降法,P只需要提供一个初值。
本质上,kalman滤波做了2件事:
基于前一时间点的系统状态的概率分布给出当前时间点的系统状态的概率分布预测P1
基于当前时间点的观测量的概率分布Q给出另一组对当前时间点系统状态的概率分布预测P2 (这里需要注意,如果传感器能直接把系统状态都观测了,那么我们直接用观测量的概率分布Q作为P2就好了,但是有可能传感器观测的物理量量并不是直接的系统状态,而是其他物理量,这时我们需要通过做一个线性变换来获得P2)
现在,我们有两个关于当前时间点系统状态的概率分布的预测P1和P2,我们于是可以计算它们的联合概率分布,也就是为什么文章中要把两个概率分布乘到一起去。这个联合概率分布就是我们最终想要的更正过后的当前时间点的系统状态概率分布,有了它我们就可以进入下一个时间点继续迭代我们交替的预测-更正步骤了
值得注意的是,卡尔曼滤波器针对于线性系统,而非线性系统则要考虑扩展卡尔曼滤波,通过雅克比矩阵对系统线性化。
卡尔曼滤波实例 对于上面的案例,你也可以参考这个视频https://www.youtube.com/watch?v=bm3cwEP2nUo,虽然其英语一股咖喱味,但口音在可接受范围内。
多维卡尔曼滤波可以参考这里:https://zhuanlan.zhihu.com/p/45238681
下面我们讨论一维卡尔曼滤波的实例。
一维卡尔曼滤波 样例:对二维平面内的位置信息进行滤波。
此处我们假设传感器读数与真实情况是相同的,不需要做任何变换,即 H k = H k T = [ 1 ] H_k=H_k^T=[1] H k = H k T = [ 1 ]
预测:
更新:
K k = P k P k + R k (19) {\color{purple}K_k}=\dfrac{ {\color{Red}P_k} }{ {\color{Red}P_k}+{\color{Turquoise}R_k} }\tag{19} K k = P k + R k P k ( 19 )
x ^ k ′ = x ^ k + K k ( z ⃗ k − x ^ k ) P k ′ = P k − K k P k (18) \begin{aligned} {\color{skyBlue}\hat x_k'} &= {\color{Magenta}\hat{x}_k}&&+{\color{purple}K_k}({\color{LimeGreen}{\vec z}_k}-{\color{Magenta}\hat{x}_k})\\ {\color{CornflowerBlue}P_k'} &= {\color{Red}P_k} &&-{\color{purple}K_k}{\color{Red}P_k} \end{aligned}\tag{18} x ^ k ′ P k ′ = x ^ k = P k + K k ( z k − x ^ k ) − K k P k ( 18 )
此处我们用 K k K_k K k k k k
x ^ k ′ = x ^ k − 1 + K k ( z ⃗ k − x ^ k − 1 ) P k ′ = P k − 1 − K k P k − 1 (19) \begin{aligned} {\color{skyBlue}\hat x_k'} &= {\color{blue}\hat x_{k-1}}&&+{\color{purple}K_k}({\color{LimeGreen}{\vec z}_k}- {\color{blue}\hat x_{k-1}})\\ {\color{CornflowerBlue}P_k'} &= {\color{blue} P_{k-1}} &&-{\color{purple}K_k}{\color{blue} P_{k-1}} \end{aligned}\tag{19} x ^ k ′ P k ′ = x ^ k − 1 = P k − 1 + K k ( z k − x ^ k − 1 ) − K k P k − 1 ( 19 )
其实式(19)就很好地解释了状态更新方程,它意味着我们接收 K k K_k K k
此处还有一个问题需要解决,即 R k {\color{Turquoise}R_k} R k R k {\color{Turquoise}R_k} R k
z k = x k + w k z_k=x_k+w_k z k = x k + w k
其中 w k w_k w k R = C o v ( w ) R=Cov(w) R = C o v ( w ) R R R
补充:协方差矩阵 协方差矩阵在统计学和机器学习中随处可见,一般而言,可视作方差 和协方差 两部分组成,即方差构成了对角线上的元素,协方差构成了非对角线上的元素。本文旨在从几何角度介绍我们所熟知的协方差矩阵。
在统计学中,方差 是用来度量单个随机变量 的离散程度 ,而协方差则一般用来刻画两个随机变量 的相似程度 ,其中,方差 的计算公式为σ x 2 = 1 n − 1 ∑ i = 1 n ( x i − x ‾ ) 2 σ_x^2=\dfrac1{n−1}∑_{i=1}^n(x_i−\overline x)^2 σ x 2 = n − 1 1 ∑ i = 1 n ( x i − x ) 2 n n n x ‾ \overline x x
在此基础上,对于x = { x 1 , x 2 , . . . , x n } , y = { y 1 , y 2 , . . . , y n } x=\{x_1,x_2,...,x_n\},y=\{y_1,y_2,...,y_n\} x = { x 1 , x 2 , ... , x n } , y = { y 1 , y 2 , ... , y n } 协方差 的计算公式被定义为
σ ( x , y ) = 1 n − 1 ∑ i = 1 n ( x i − x ‾ ) ( y i − y ‾ ) σ(x,y)=\dfrac 1 {n−1}∑_{i=1}^n(x_i−\overline x)(y_i−\overline y) σ ( x , y ) = n − 1 1 ∑ i = 1 n ( x i − x ) ( y i − y )
在公式中,符号 x ‾ \overline x x y ‾ \overline y y σ x 2 σ_x^2 σ x 2 x x x σ ( x , x ) σ(x,x) σ ( x , x )
从方差/协方差到协方差矩阵 根据方差的定义,给定 d d d x k , k = 1 , 2 , . . . , d x_k,k=1,2,...,d x k , k = 1 , 2 , ... , d 随机变量的方差 为
σ ( x k , x k ) = 1 n − 1 ∑ i = 1 n ( x k i − x ‾ k ) 2 , k = 1 , 2 , . . . , d σ(x_k,x_k)=\dfrac 1 {n−1}∑_{i=1}^n(x_{ki}−\overline x_k)^2,k=1,2,...,d σ ( x k , x k ) = n − 1 1 ∑ i = 1 n ( x ki − x k ) 2 , k = 1 , 2 , ... , d
其中,为方便书写, x k i x_{ki} x ki x k x_k x k i i i n n n n n n
对于这些随机变量,我们还可以根据协方差的定义,求出 d d d
σ ( x m , x k ) = 1 n − 1 ∑ i = 1 n ( x m i − x ‾ m ) ( x k i − x ‾ k ) , m , n ∈ [ 1 , d ] σ(x_m,x_k)=\dfrac1{n−1}∑_{i=1}^n(x_{mi}−\overline x_m)(x_{ki}−\overline x_k),m,n\in[1,d] σ ( x m , x k ) = n − 1 1 ∑ i = 1 n ( x mi − x m ) ( x ki − x k ) , m , n ∈ [ 1 , d ]
因此,协方差矩阵 为
∑ = [ σ ( x 1 , x 1 ) ⋯ σ ( x 1 , x d ) ⋮ ⋱ ⋮ σ ( x d , x 1 ) ⋯ σ ( x d , x d ) ] ∈ R d × d \sum=\left[ \begin{matrix} σ(x_1,x_1)&⋯&σ(x_1,x_d) \\ ⋮&⋱&⋮ \\ σ(x_d,x_1)&⋯&σ(x_d,x_d) \end{matrix} \right]∈R^{d×d} ∑ = ⎣ ⎡ σ ( x 1 , x 1 ) ⋮ σ ( x d , x 1 ) ⋯ ⋱ ⋯ σ ( x 1 , x d ) ⋮ σ ( x d , x d ) ⎦ ⎤ ∈ R d × d
其中,对角线上的元素为各个随机变量的方差,非对角线上的元素为两两随机变量之间的协方差,根据协方差的定义,我们可以认定:矩阵 Σ Σ Σ 对称矩阵 (symmetric matrix),其大小为 d × d d×d d × d
从期望计算协方差 期望值分别为 E [ X ] E[X] E [ X ] E [ Y ] E[Y] E [ Y ] X X X Y Y Y 协方差 C o v ( X , Y ) Cov(X,Y) C o v ( X , Y )
C o v ( X , Y ) = E [ ( X − E [ X ] ) ( Y − E [ Y ] ) ] = E [ X Y ] − 2 E [ Y ] E [ X ] + E [ X ] [ Y ] = E [ X Y ] − E [ X ] [ Y ] \begin{aligned} Cov(X,Y) &= E[(X-E[X])(Y-E[Y])] \\ &= E[XY]-2E[Y]E[X]+E[X][Y]\\ &=E[XY]-E[X][Y] \end{aligned} C o v ( X , Y ) = E [( X − E [ X ]) ( Y − E [ Y ])] = E [ X Y ] − 2 E [ Y ] E [ X ] + E [ X ] [ Y ] = E [ X Y ] − E [ X ] [ Y ]
如果两个变量的变化趋势一致,也就是说如果其中一个大于自身的期望值时另外一个也大于自身的期望值,那么两个变量之间的协方差就是正值;如果两个变量的变化趋势相反,即其中一个变量大于自身的期望值时另外一个却小于自身的期望值,那么两个变量之间的协方差就是负值。
如果 X X X Y Y Y E [ X Y ] = E [ X ] E [ Y ] E[XY]=E[X]E[Y] E [ X Y ] = E [ X ] E [ Y ]
但是,反过来并不成立。即如果 X X X Y Y Y
补充:均值与期望 由于语言等方面的原因,通常人们口中说到均值的时候,是在谈论平均值。因此,以上的混乱事实上是对平均值和期望的混乱。而平均值属于《数理统计》的范畴,期望属于《概率论》的范畴,因此,这种混淆更深层次的反映出人们对这两门学科理解的混乱。由于在学习相关知识的时候教材通常是《概率论与数理统计》,由于概率论与数理统计联系十分紧密,出版社将这两门学科安排在了同一本书中。对于懵懂的新生来说,都是一本书、一堂课、一个教学老师,对于习惯了以前不同科目不同老师的划分方式,这样的内容安排以及教学安排是很难接受的。学生在思维上没有及时转变过来,因此,混淆这两者的关系就是情理之中了。
二者的区别 均值是针对实验观察到的特征样本而言的,是统计学概念。期望是针对于随机变量总体而言的一个量,是样本值与出现概率之积的求和,是一个统计量(对观察样本的统计),期望是一种概率论概念,是一个数学特征。
均值是一个统计量(对观察样本的统计),期望是一种概率论概念,是一个数学特征。
例如我们进行掷骰子,掷了六次,点数分别为2,2,2,4,4,4,这六次的观察就是我们的样本 ,于是我们可以说为均值为 2 + 2 + 2 + 4 + 4 + 4 6 = 3 \dfrac{2+2+2+4+4+4}{6}=3 6 2 + 2 + 2 + 4 + 4 + 4 = 3
但其期望是:E ( X ) = 1 × 1 6 + 2 × 1 6 + 3 × 1 6 + 4 × 1 6 + 5 × 1 6 + 6 × 1 6 = 3.5 E(X)=1\times\dfrac1 6+2\times\dfrac1 6+3\times\dfrac1 6+4\times\dfrac1 6+5\times\dfrac1 6+6\times\dfrac1 6=3.5 E ( X ) = 1 × 6 1 + 2 × 6 1 + 3 × 6 1 + 4 × 6 1 + 5 × 6 1 + 6 × 6 1 = 3.5
二者的联系 平均值和中位数、众数、中点距被一起用来描述一组样本的中心趋势,是样本集合的一种中心化趋势的描述。期望的描述引述陈希孺院士《概率论与数理统计》如下:
数学期望 常称为“均值”,即“随机变量取值的平均值”之意,当然这个平均,是指以概率为权的加权平均。……数学期望是由随机变量的分布完全决定。
以上表明数学期望是随机变量的一种中心化趋势的描述。如果认为平均值和期望相同,大脑只需对一个点进行记忆;如果不同,就需要对两个点进行记忆,更何况是随机变量这种十分抽象的概念。因此,忽视前面的修饰(样本集合、随机变量)就是十分普遍的事情了。
大数定理说明当样本量N趋近无穷大的时候,样本的平均值无限接近数学期望。
In probability theory, the law of large numbers (LLN) is a theorem that describes the result of performing the same experiment a large number of times. According to the law, the average of the results obtained from a large number of trials should be close to the expected value, and will tend to become closer as more trials are performed.
这里有一个限定条件“样本量趋近无穷大”,往往人们容易遗忘的就是这个限定条件。如果样本较小的时候,使用平均值来代替期望就要计算它可信程度了(置信水平)。
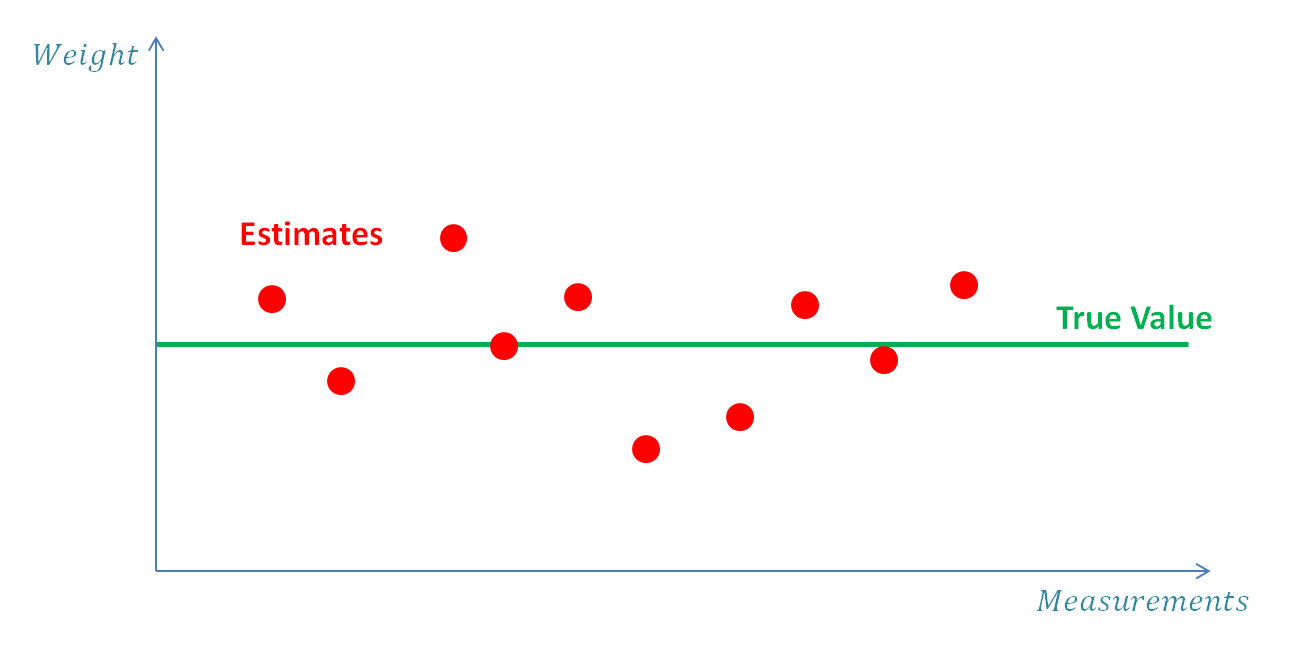
补充:α − β − γ \alpha-\beta-\gamma α − β − γ 金条重量:α \alpha α 在这个例子中,我们要估计静态系统的状态。静态系统是指在相当一段时间内不改变状态的系统。在本例中,我们将估计金条的重量。我们将使用一个无偏秤,也就是说,它没有系统误差,但有随机噪声。
在本例中,系统是金条,系统的状态就是金条的重量。假设金条的重量在短时间内不发生变化,即系统的动态模型是恒定的 。为了估计系统的状态(金条的重量),可以进行多次测量并求平均值。
经过 n n n x ^ n , n \hat x_{n,n} x ^ n , n
x ^ n , n = 1 n ( z 1 + z 2 + … + z n − 1 + z n ) = 1 n ∑ i = 1 n ( z i ) (21) \hat x_{n,n}=\dfrac{1}n(z_1+z_2+…+z_n−1+z_n)=\dfrac{1}{n}\sum_{i=1}^n(z_i)\tag {21} x ^ n , n = n 1 ( z 1 + z 2 + … + z n − 1 + z n ) = n 1 i = 1 ∑ n ( z i ) ( 21 )
另外,z i z_i z i i i i x ^ n , n \hat x_{n,n} x ^ n , n n n n x x x z n z_n z n x ^ n , n − 1 \hat x_{n,n-1} x ^ n , n − 1 x x x z n − 1 z_{n-1} z n − 1 x ^ n + 1 , n \hat x_{n+1,n} x ^ n + 1 , n ( n + 1 ) (n+1) ( n + 1 ) x x x z n z_n z n
本例中的动态模型是定值,所以 x ^ n + 1 , n = x ^ n , n \hat x_{n+1,n}=\hat x_{n,n} x ^ n + 1 , n = x ^ n , n ,也就是说,在测量出 z n z_n z n x ^ n , n \hat x_{n,n} x ^ n , n x n + 1 , n x_{n+1,n} x n + 1 , n
我们希望找到一种方法,仅通过 x ^ n − 1 , x − 1 \hat x_{n-1,x-1} x ^ n − 1 , x − 1 z n z_n z n x ^ n , n \hat x_{n,n} x ^ n , n
x ^ n , n = 1 n ∑ i = 1 n ( z i ) = 1 n ( z n + ∑ i = 1 n − 1 ( z i ) ) = 1 n ⋅ n − 1 n − 1 ⋅ ∑ i = 1 n − 1 ( z i ) + 1 n ⋅ z n = n − 1 n ⋅ ( 1 n − 1 ⋅ ∑ i = 1 n − 1 ( z i ) ) + 1 n ⋅ z n = n − 1 n ⋅ x ^ n − 1 , n − 1 + 1 n ⋅ z n = x ^ n − 1 , n − 1 + 1 n ( z n − x ^ n − 1 , n − 1 ) \begin{aligned} \hat x_{n,n} &= \dfrac{1}{n}\sum_{i=1}^n(z_i)\\ &= \dfrac1 n(z_n+\sum_{i=1}^{n-1}(z_i))\\ &= \dfrac{1}{n}\cdot\dfrac{n-1}{n-1}\cdot\sum_{i=1}^{n-1}(z_i)+\dfrac{1}{n}\cdot z_n\\ &= \dfrac{n-1}{n}\cdot\bigg(\dfrac{1}{n-1}\cdot \sum_{i=1}^{n-1}(z_i)\bigg)+\dfrac{1}{n}\cdot z_n\\ &= \dfrac{n-1}{n}\cdot \hat x_{n-1,n-1}+\dfrac{1}{n}\cdot z_n\\ &= \hat x_{n-1,n-1} + \dfrac 1 n(z_n-\hat x_{n-1,n-1}) \end{aligned} x ^ n , n = n 1 i = 1 ∑ n ( z i ) = n 1 ( z n + i = 1 ∑ n − 1 ( z i )) = n 1 ⋅ n − 1 n − 1 ⋅ i = 1 ∑ n − 1 ( z i ) + n 1 ⋅ z n = n n − 1 ⋅ ( n − 1 1 ⋅ i = 1 ∑ n − 1 ( z i ) ) + n 1 ⋅ z n = n n − 1 ⋅ x ^ n − 1 , n − 1 + n 1 ⋅ z n = x ^ n − 1 , n − 1 + n 1 ( z n − x ^ n − 1 , n − 1 )
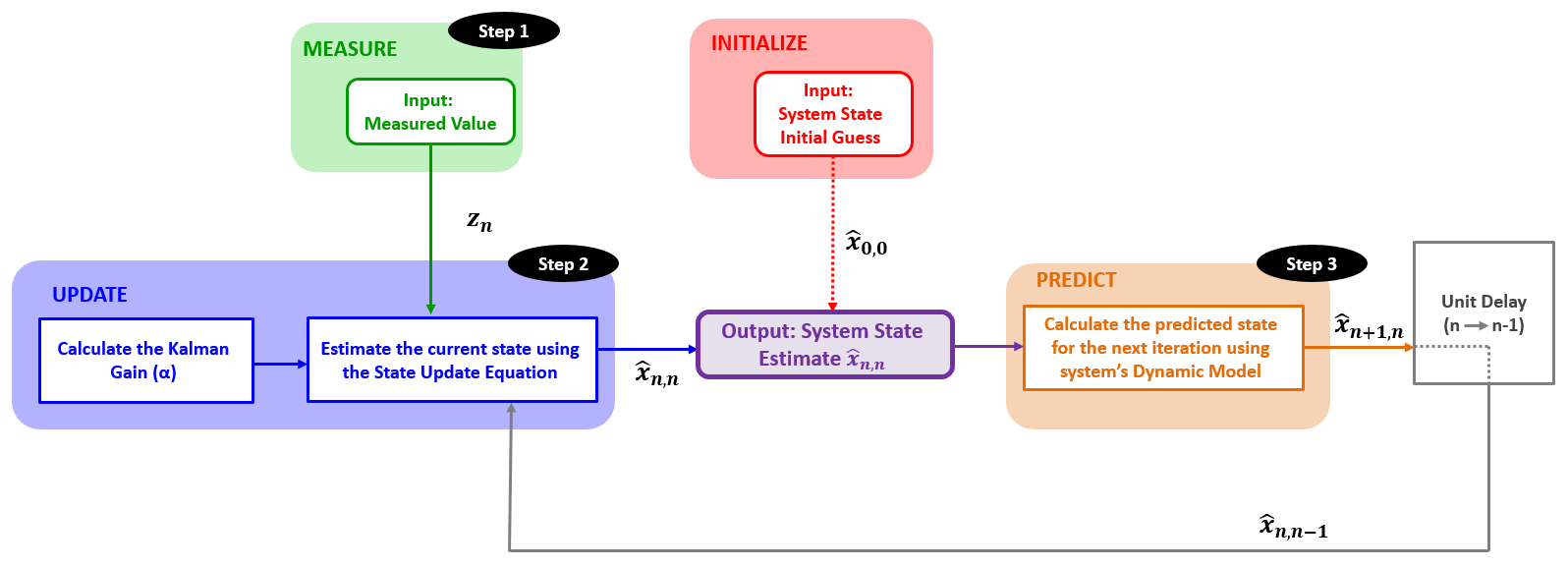
上面方程对应卡尔曼滤波五个方程之一,名为状态更新 State Update Equation 。其含义为:
系数 1 n \dfrac1 n n 1 卡尔曼增益 Kalman Gain 。我们暂时会使用希腊字母 α n α_n α n K n K_n K n
也就是说,状态更新方程如下(动态模型是定值所以忽略是何时进行估计):
x ^ n , n = x ^ n − 1 , n − 1 + α n ( z n − x ^ n − 1 , n − 1 ) x ^ n = x ^ n − 1 + α n ( z n − x ^ n − 1 ) \hat x_{n,n}=\hat x_{n-1,n-1}+\alpha_n(z_n-\hat x_{n-1,n-1})\\ \hat x_n=\hat x_{n-1}+\alpha_n(z_n-\hat x_{n-1}) x ^ n , n = x ^ n − 1 , n − 1 + α n ( z n − x ^ n − 1 , n − 1 ) x ^ n = x ^ n − 1 + α n ( z n − x ^ n − 1 )
其中 ( z n − x ^ n − 1 ) (z_n-\hat x_{n-1}) ( z n − x ^ n − 1 ) 更新innovation ,更新包含了新的信息。
本例中, 1 n \dfrac 1 n n 1 n n n 1 n \dfrac 1 n n 1
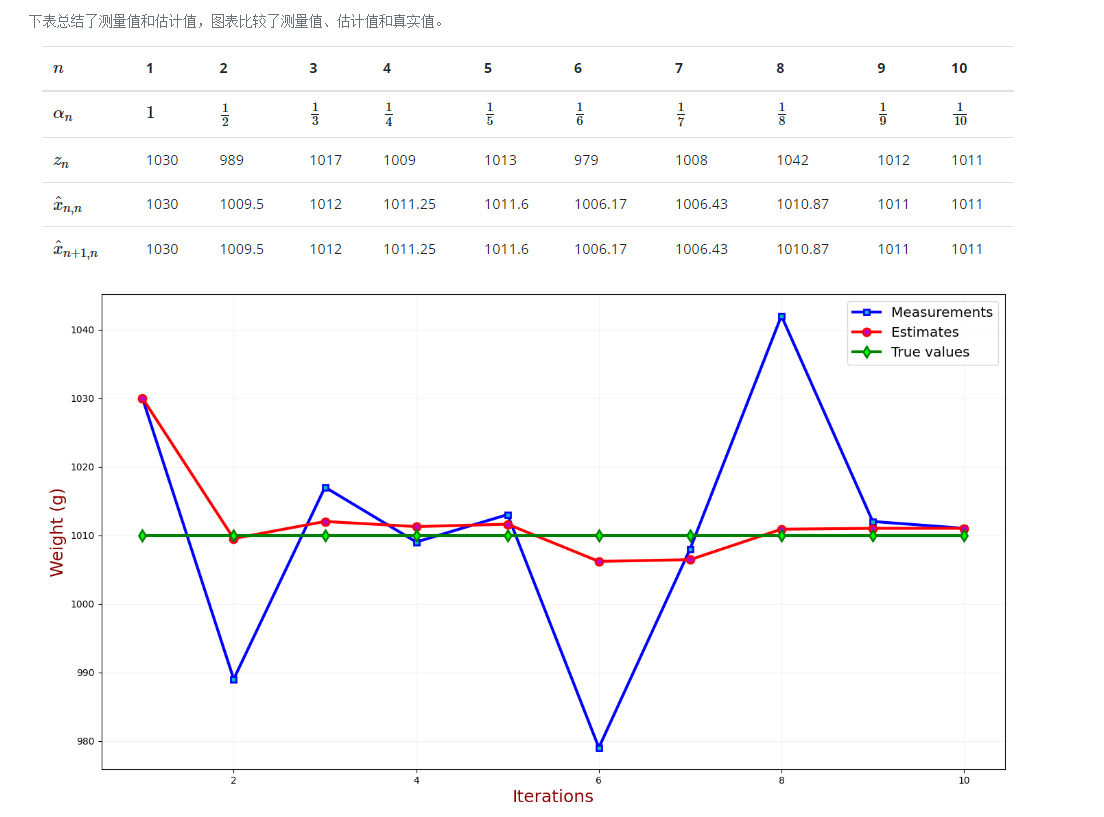
实例 第零次迭代 初始化 我们对金条重量的初步估计是1000克。滤波器初始化操作仅需一次,不会用在下一次迭代中。
x 0 = 1000 g x_0=1000g x 0 = 1000 g
预测 金条的重量是不变的,因此系统的动态模型是静态的,状态的下一个估计值(预测值)等于初始值:
x ^ 1 , 0 = x ^ 0 , 0 = 1000 g \hat x_{1,0}=\hat x_{0,0} =1000g x ^ 1 , 0 = x ^ 0 , 0 = 1000 g
或者,更直接的,x ^ 1 = 1000 g \hat x_1=1000g x ^ 1 = 1000 g
第一次迭代 测量 第一次秤重:z 1 = 1030 g z_1=1030g z 1 = 1030 g
更新 计算增益,α n = 1 n , α 1 = 1 \alpha_n=\dfrac1 n,\alpha_1=1 α n = n 1 , α 1 = 1
状态更新方程计算当前估计值 x ^ 1 , 1 = x ^ 1 , 0 + α 1 ( z 1 − x ^ 1 , 0 ) = 1030 g \hat x_{1,1}=\hat x_{1,0}+\alpha_1(z_1-\hat x_{1,0})=1030g x ^ 1 , 1 = x ^ 1 , 0 + α 1 ( z 1 − x ^ 1 , 0 ) = 1030 g
估计 系统的动态模型是静态的,因此金条的重量不会改变,状态的下一个估计值(预测值)等于当前的估计值:
x ^ 2 , 1 = x ^ 1 , 1 = 1030 g \hat x_{2,1}=\hat x_{1,1}=1030g x ^ 2 , 1 = x ^ 1 , 1 = 1030 g
或者说,x ^ 2 = 1030 g \hat x_2=1030g x ^ 2 = 1030 g
第二次迭代 经过一个单位时间后,上一次迭代的预测值predicted estimate 将成为当前迭代的先验估计值previous estimate
测量 第一次秤重:z 2 = 989 g z_2=989g z 2 = 989 g
更新 计算增益,α 2 = 1 \alpha_2=1 α 2 = 1
状态更新方程计算当前估计值 x ^ 2 , 2 = x ^ 2 , 1 + α 2 ( z 2 − x ^ 2 , 1 ) = 1009.5 g \hat x_{2,2}=\hat x_{2,1}+\alpha_2(z_2-\hat x_{2,1})=1009.5g x ^ 2 , 2 = x ^ 2 , 1 + α 2 ( z 2 − x ^ 2 , 1 ) = 1009.5 g
估计 系统的动态模型是静态的,因此金条的重量不会改变,状态的下一个估计值(预测值)等于当前的估计值:
x ^ 3 , 2 = x ^ 2 , 2 = 1009.5 g \hat x_{3,2}=\hat x_{2,2}=1009.5g x ^ 3 , 2 = x ^ 2 , 2 = 1009.5 g
或者说,x ^ 3 = 1009.5 g \hat x_3=1009.5g x ^ 3 = 1009.5 g
以此类推。
当然这个例子是最简单的例子,如果想了解更多可以参考https://www.kalmanfilter.net/CN/alphabeta_cn.html
参考 卡尔曼滤波
http://www.bzarg.com/p/how-a-kalman-filter-works-in-pictures/
https://blog.csdn.net/callmeup/category_11494879.html
α − β − γ \alpha-\beta-\gamma α − β − γ
https://www.kalmanfilter.net/CN/alphabeta_cn.html
协方差矩阵
https://zhuanlan.zhihu.com/p/37609917
均值与期望
https://blog.csdn.net/wangyaninglm/article/details/80197579
https://zhuanlan.zhihu.com/p/34150914