cs224w-图机器学习1

Introduction

选择图的原因：图是用于描述并分析有关联 / 互动的实体的一种普适语言。它不将实体视为一系列孤立的点，而认为其互相之间有关系。它是一种很好的描述领域知识的方式。

网络与图的分类

  1. networks / natural graphs：自然表示为图
    1. Social networks: Society is a collection of 7+ billion individuals
    2. Communication and transactions: Electronic devices, phone calls, financial transactions
    3. Biomedicine: Interactions between genes/proteins regulate life（大概是基因或蛋白质之间互动从而调节生理活动的过程）
    4. Brain connections: Our thoughts are hidden in the connections between billions of neurons
  2. graphs：作为一种表示方法
    1. Information/knowledge are organized and linked
    2. Software can be represented as a graph
    3. Similarity networks: Connect similar data points
    4. Relational structures: Molecules, Scene graphs, 3D shapes, Particle-based physics simulations
  3. 有时 network 和 graph 之间的差别是模糊的

传统深度学习与图神经网络

这里相对图而言，文本、图片等甚至是更结构化的数据，它们都能在特定维度下进行规则的表示

复杂领域会有丰富的关系结构，可以被表示为关系图 relational graph，通过显式地建模关系，可以获得更好的表现但是现代深度学习工具常用于建模简单的序列 sequence（如文本、语音等具有线性结构的数据）和 grid（图片具有平移不变性，可以被表示为 fixed size grids 或 fixed size standards） 这些传统工具很难用于图的建模，其难点在于网络的复杂：

  • 任意的大小和复杂的拓扑结构（即，没有像图像那样的空间局部性）

  • 没有基准点，没有节点固定的顺序。没有那种上下左右的方向

  • 经常出现动态的图，而且会有多模态的特征

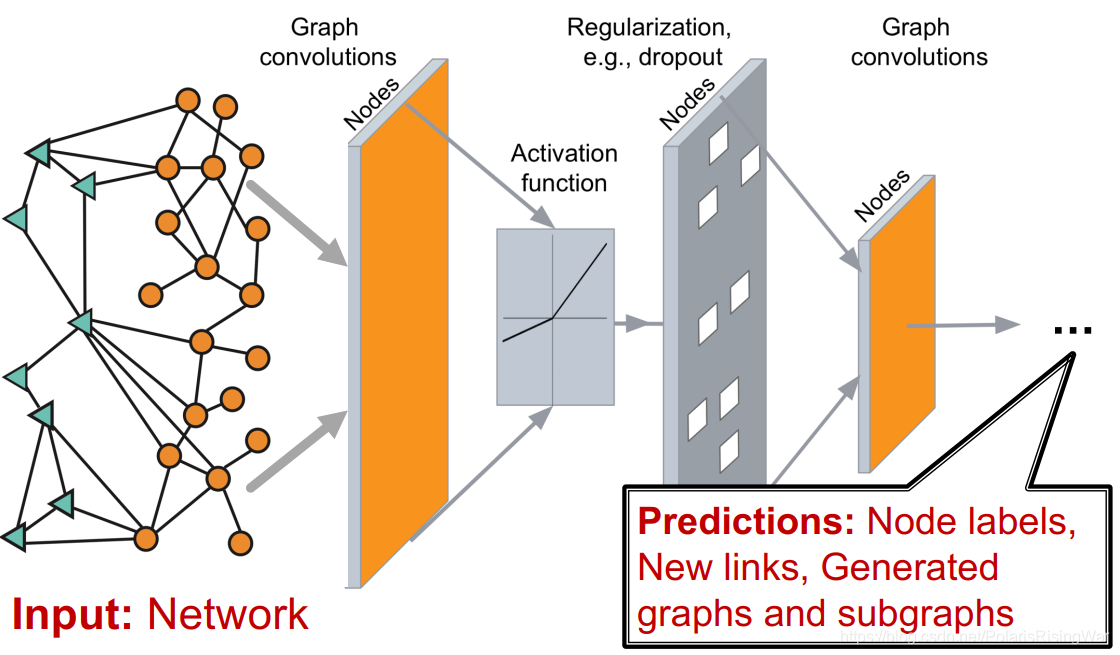
图神经网络基本模型如下，我们输入一张图，输出预测的结果，所以关键点就在于如何设计中间的神经网络

  1. 监督机器学习全流程图：

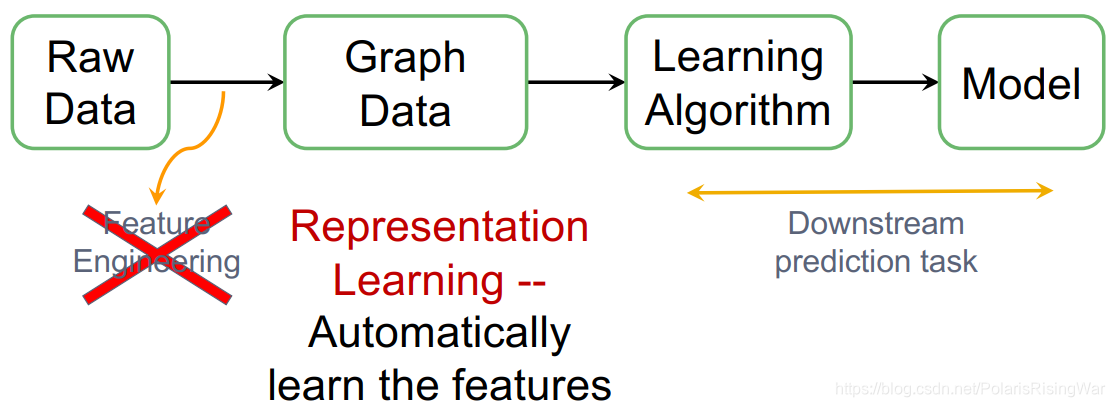
    在传统机器学习流程中，我们需要对原始数据进行特征工程 feature engineering（比如手动提取特征等)，但是现在我们使用表示学习 representation learning 的方式来自动学习到数据的特征，直接应用于下游预测任务，这杨就相当于删除了功能工程步骤

  2. 图的表示学习：大致来说就是将原始的节点（或链接、或图）表示为向量（嵌入 embedding），图中相似的节点会被 embed 得靠近（指同一实体，在节点空间上相似，在向量空间上就也应当相似）

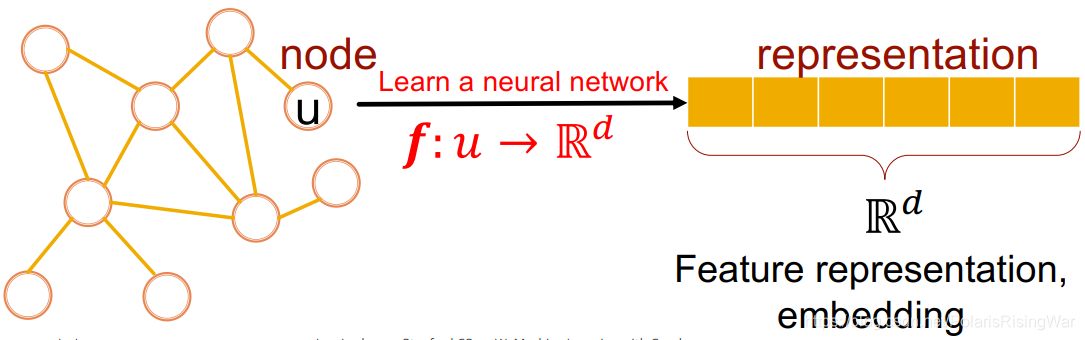
    我们可以想到的表征学习的方法是映射我们图的节点到d维嵌入，或者说到d维向量，这样看起来好像是网络中的节点紧密地嵌入到嵌入空间中。因此，目标是学习将要使用的函数f，将节点映射到这些d维实值向量中，这个向量会在这里称呼它为一个representation，或给定节点的特征表示或嵌入，再到整个图的嵌入，给定链接的嵌入，依此类推。

  3. cs224w 本课程将聚焦图的机器学习和表示学习多个领域，课程大纲如下：

    1. Traditional methods: Graphlets, Graph Kernels
    2. Methods for node embeddings: DeepWalk, Node2Vec
    3. Graph Neural Networks: GCN, GraphSAGE, GAT, Theory of GNNs
    4. Knowledge graphs and reasoning: TransE, BetaE
    5. Deep generative models for graphs
    6. Applications to Biomedicine, Science, Industry

Applications of Graph ML

四类图机器学习任务

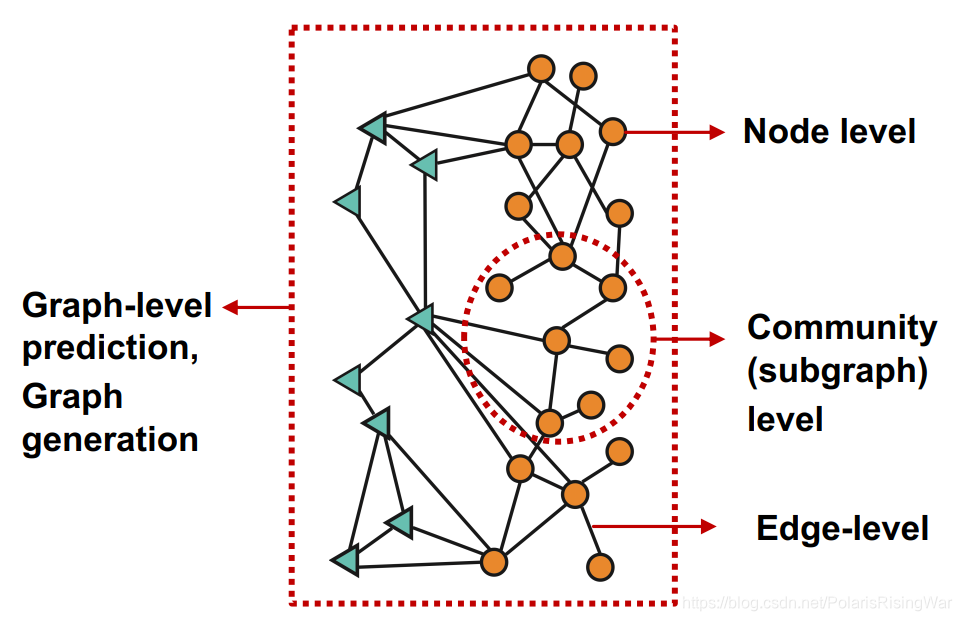
  1. 节点级别 node level
  2. 边级别 edge level
  3. 社区 / 子图级别 community(subgraph) level
  4. 图级别，包括预测任务 graph-level prediction 和 图生成任务 graph generation

各类型的典型任务

  • 节点分类：预测节点的属性

    • 示例：对在线用户/物品进行分类

  • 链接预测：预测两个节点之间是否存在缺失的链接

    • 示例：知识图谱完善

  • 图分类：对不同的图进行分类

    • 示例：分子属性预测

  • 聚类：检测节点是否形成一个社区

    • 示例：社交网络

  • 其他任务

    • 图生成：药物发现
    • 图演化：物理模拟

Choice of Graph Representation

数据结构知识及其应用

Traditional Methods for ML on Graphs

传统机器学习中图的应用

章节前言

对于图机器学习，我们要调查的是不同级别的任务：我们可以考虑节点级别的预测任务，我们可以考虑链接级别或边缘级别的预测任务，比如考虑成对的节点并尝试预测该对节点是否已连接。我们可以考虑图形级预测，比如我们想要对整个图形进行预测。

传统机器学习 pipeline：设计并获取所有训练数据上节点 / 边 / 图的特征→训练机器学习模型→应用模型

图数据本身就会有特征/属性，但是我们还想获得说明其在网络中的位置、其局部网络结构 local network structure 之类的特征（这些额外的特征描述了网络的拓扑结构，能使预测更加准确） 。所以最终一共有两种特征：数据的 structural feature，以及其本身的 attributes and properities

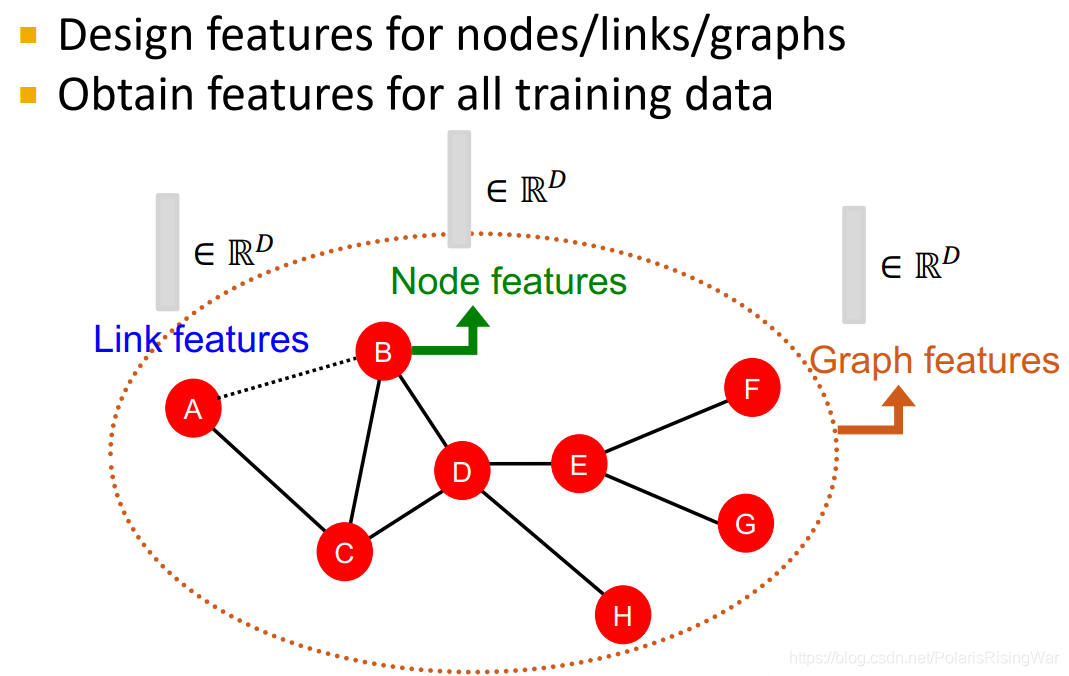
本章重点着眼于手工设计无向图三种数据层次上的特征（其 relational structure of the network），做预测问题

design choice

  1. Features: d-dimensional vectors
  2. Objects: Nodes, edges, sets of nodes, entire graphs
  3. Objective function: What task are we aiming to solve?

Traditional Feature-based Methods: Node

我们可以想到的方式是，我们将一个图作为一组顶点和边的集合，我们想学习一个函数，每一个节点都会给我们一个真实的预测，也即：给定 G=(V,E)G=(V,E) ，找到 f:V→Rf:V\to \mathbb R。问题是，我们如何学习该功能，ff 会做出这些预测吗？

特征抽取

目标：找到能够描述节点在网络中结构与位置的特征，也就是说目标是表征给定节点周围的网络结构，以及某种意义上节点在更广泛的网络环境中的位置。我们将讨论四个不同的使我们能够做到这一点的方法。

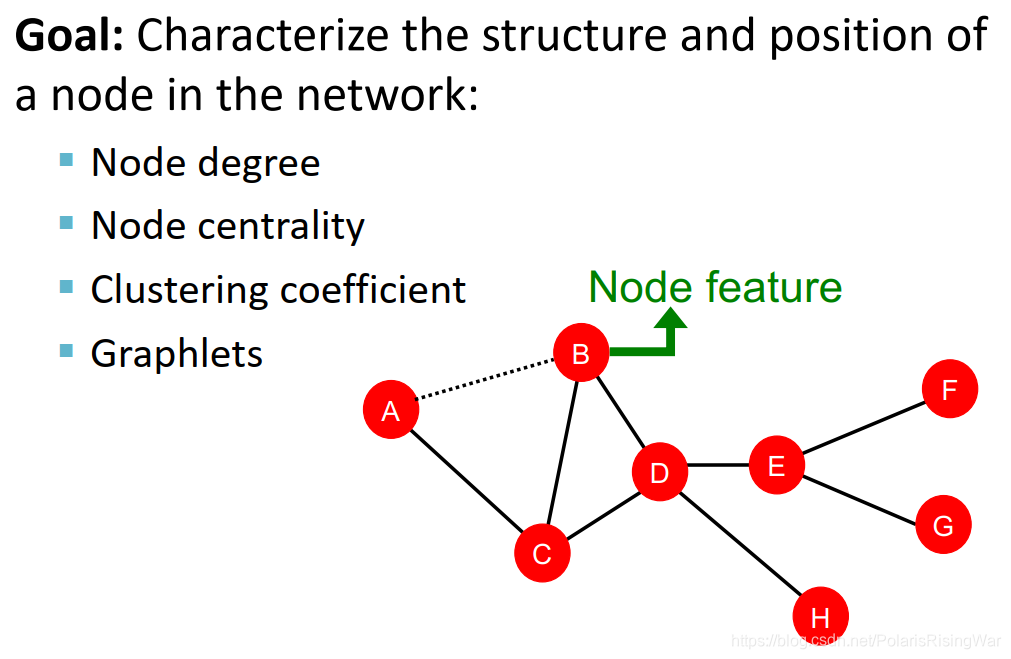
node degree

缺点在于仅考虑所有相邻节点，且将节点的所有邻居视为同等重要的

node centrality cvc_v

考虑了节点的重要性，几种衡量方法如下

  • eigenvector centrality：认为如果节点邻居重要，那么节点本身也重要

    • 因此节点 vv 的 centrality 是邻居 centrality 的加总： cv=1λ∑u∈N(v)cuc_v=\frac{1}{\lambda}\sum\limits_{u\in N(v)}c_u（ λ\lambda 是某个正的常数）

    • 这是个递归式，解法是将其转换为矩阵形式： λc=Ac\lambda \mathbf{c}=\mathbf{Ac}，A\mathbf{A} 是邻接矩阵，c\mathbf{c} 是 centralty 向量。

    • 从而发现 centrality 就是特征向量。根据 Perron-Frobenius Theorem2 可知最大的特征值 $ \lambda_{max}$​ 总为正且唯一，对应的 leading eigenvector cmax\mathbf{c}_{max} ​就是 centrality 向量

  • betweenness centrality：认为如果一个节点处在很多节点对的最短路径上，那么这个节点是重要的。地处交通要道

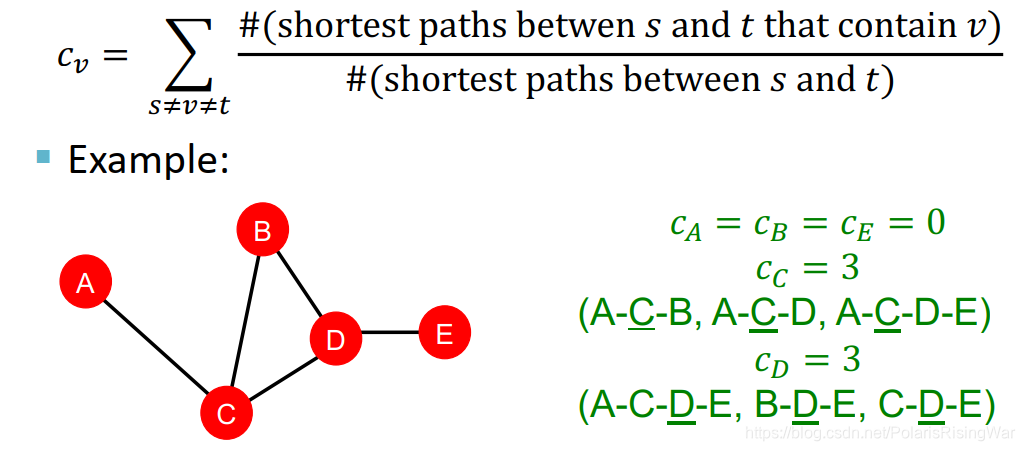
    • cv=∑s≠v≠t#(s和t之间包含v的最短路径)#(s和t之间的最短路径)c_v=\sum\limits_{s\neq v\neq t}\frac{\#(s 和 t 之间包含 v 的最短路径)}{\#(s 和 t 之间的最短路径)}

    • 意思是：the number of…

    • 图中这个 between 应该是写错了……

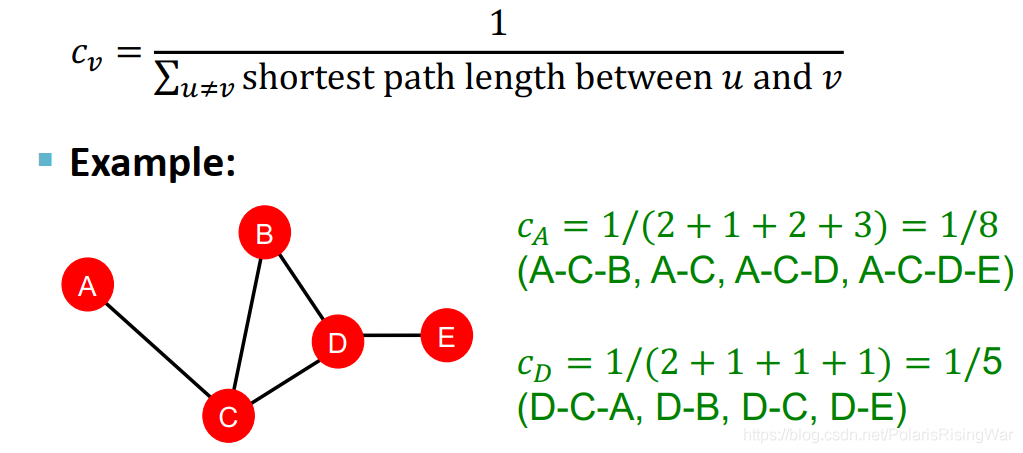
  • closeness centrality：认为如果一个节点距其他节点之间距离最短，那么认为这个节点是重要的

    • cv=1∑u≠vu和v之间的最短距离c_v=\frac{1}{\sum\limits_{u\neq v}u 和 v 之间的最短距离}

clustering coefficient

衡量节点邻居的连接程度 描述节点的局部结构信息

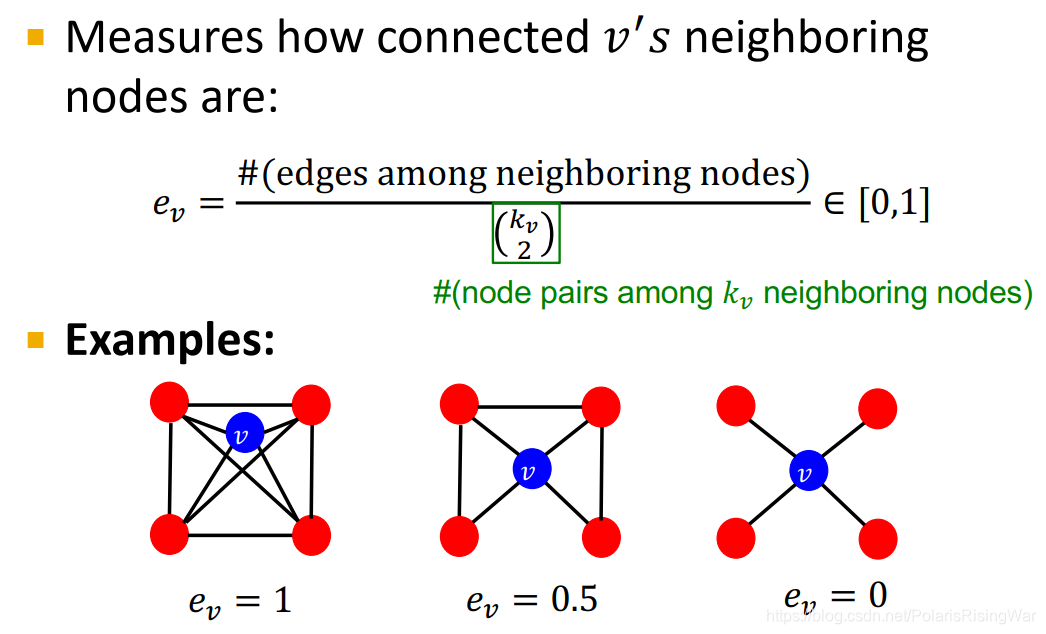
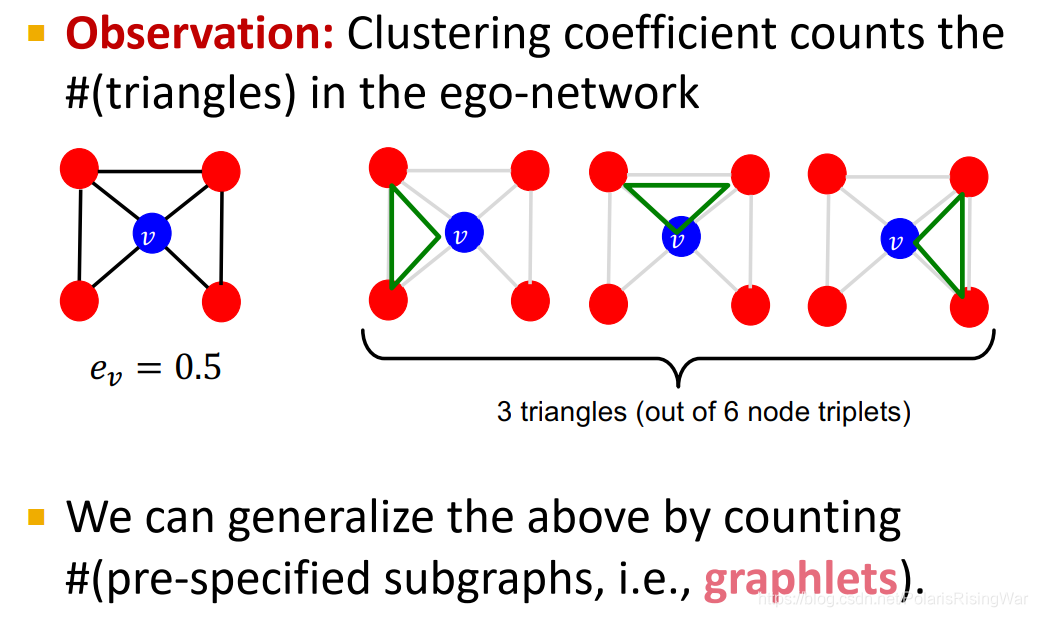
这种$$\begin{pmatrix} k_{v} \ 2 \end{pmatrix}$$是组合数的写法，和国内常用的 C 写法上下是相反的。所以这个式子代表 vv 邻居所构成的节点对，即潜在的连接数。整个公式衡量节点邻居的连接有多紧密。第 1 个例子： ev=6/6e_v=6/6 第 2 个例子： ev=3/6e_v=3/6 第 3 个例子： ev=0/6e_v=0/6

graphlets 有根连通异构子图

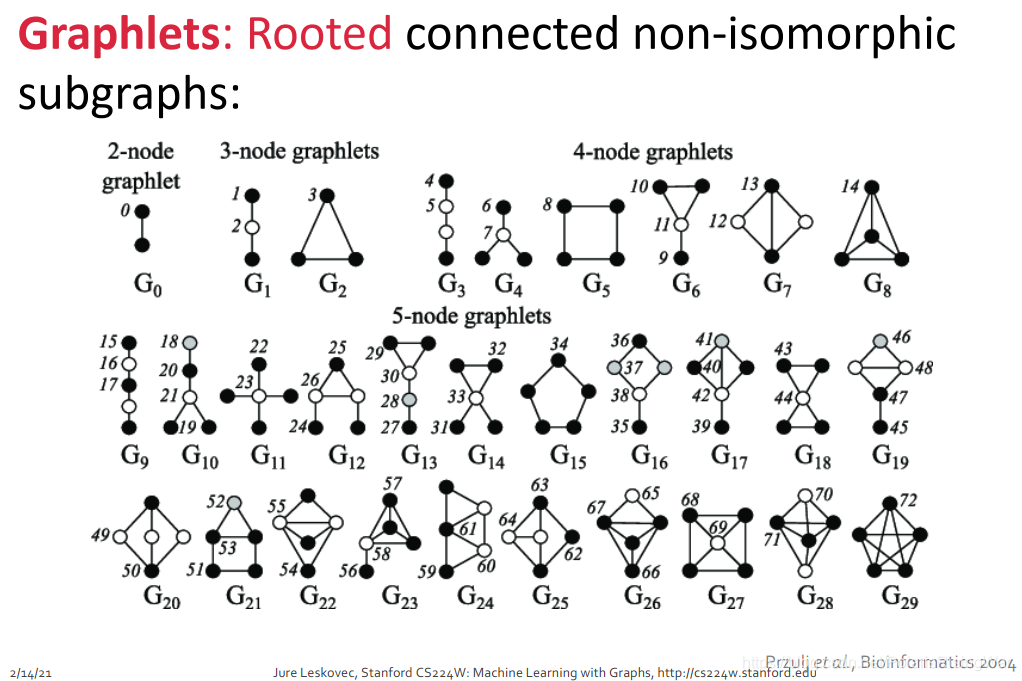
对于某一给定节点数 kk，会有 nkn_k​ 个连通的异构子图。 就是说，这些图首先是 connected 的，其次这些图有 k 个节点，第三它们异构。

图中标的数字代表根节点可选的位置。例如对于 G0G_0​，两个节点是等价的，所以只有一种 graphlet；对于 G1G_1​，根节点有在中间和在边上两种选择，上下两个边上的点是等价的，所以只有两种 graphlet。其他的类似。节点数为 2-5 情况下一共能产生如图所示 73 种 graphlet。

这 73 个 graphlet 的核心概念就是不同的形状，不同的位置。

注意这里的 graphlet 概念和后文图的 graphlet kernel 的概念不太一样。具体的后文再讲

Graphlet Degree Vector (GDV): Graphlet-base features for nodes GDV 与其他两种描述节点结构的特征的区别：

  • Degree counts #(edges) that a node touches

  • Clustering coefficient counts #(triangles) that a node touches.

  • GDV counts #(graphlets) that a node touches

  • 度：节点连接的边的数量

  • 聚类系数：节点连接的三角形的数量

  • GDV：节点连接的图元的数量

Graphlet Degree Vector (GDV): A count vector of graphslets rooted at a given node.一个以给定节点为根的图元计数向量。

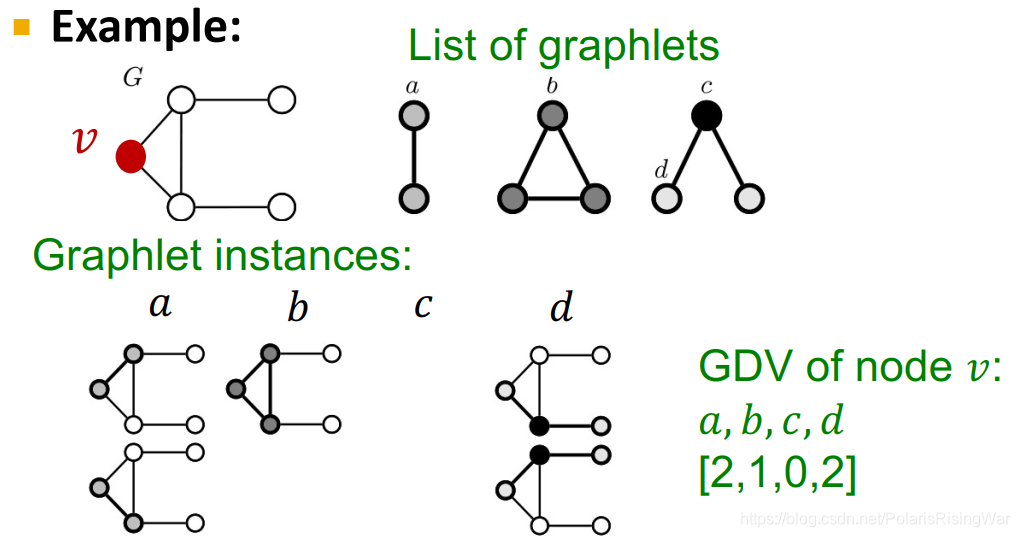
如图所示，对四种 graphlet， vv 的每一种 graphlet 的数量作为向量的一个元素。

注意：graphlet c 的情况不存在，是因为像 graphlet b 那样中间那条线连上了。这是因为 graphlet 是 induced subgraph，所以那个边也存在，所以 c 情况不存在。

考虑 2-5 个节点的 graphlets，我们得到一个长度为 73 个坐标 coordinate（就前图所示一共 73 种 graphlet）的向量 GDV，描述该点的局部拓扑结构 topology of node’s neighborhood，可以捕获距离为 4 hops 的互联性 interconnectivities。

相比节点度数或 clustering coefficient，GDV 能够描述两个节点之间更详细的节点局部拓扑结构相似性 local topological similarity。

Node Level Feature: Summary

这些特征可以分为两类：

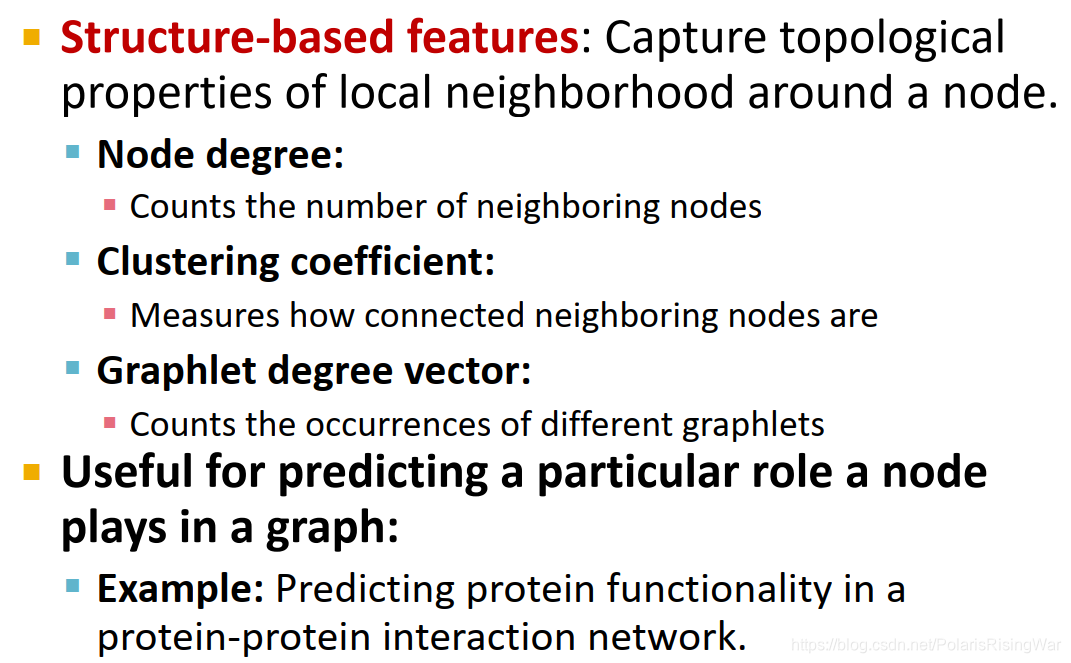
  1. Importance-based features: 捕获节点在图中的重要性

  2. Structure-based features: 捕获节点附近的拓扑属性

Discussion

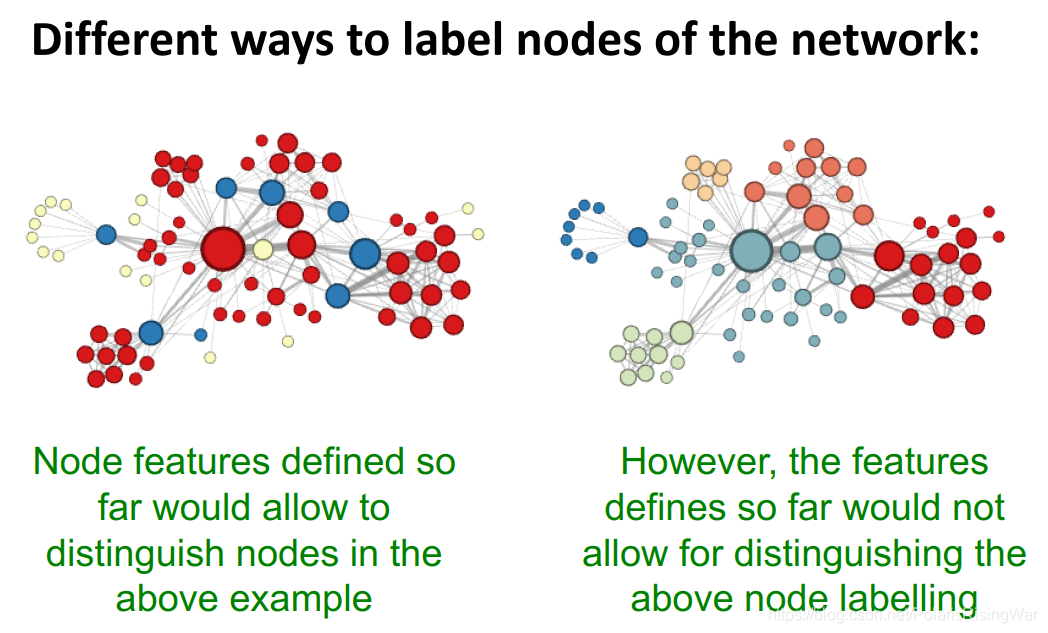
就我的理解，大致来说，传统节点特征只能识别出结构上的相似，不能识别出图上空间、距离上的相似

预测任务是基于已知的边，预测新链接的出现。测试模型时，将每一对无链接的点对进行排序，取存在链接概率最高的 K 个点对，作为预测结果

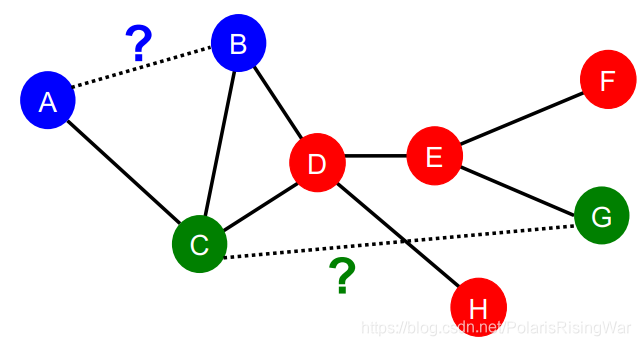
所关注的特征在点对上。有时你也可以直接将两个点的特征合并 concatenate 起来作为点对的特征，来训练模型。但这样做的缺点就在于失去了点之间关系的信息。

因此，我们对链接预测任务的看法是双向的，我们可以用两种不同的方式来表述它。我们可以这样表述一种方法：
对网络中的链接进行随机缺失，也就是说我们有一个网络，我们要随机删除一些链接，然后尝试预测（类似dropout？），

然后，公式的另一种类型是我们将随着时间的推移预测链接。这意味着，例如，如果我们拥有随时间自然发展的网络，我们的引文网络，我们的社交网络，或我们的协作网络，那我们可以说，我们来看看time zero 和 time zero prime之间的图表，基于边和结构直到时间 t0t_0 prime，然后，我们将输出的排名列表来预测某些链接将在将来出现。

所以，链接预测任务的两种类型：随机缺失边；随时间演化边

图中的 ’ 念 prime

第一种假设可以以蛋白质之间的交互作用举例，缺失的是研究者还没有发现的交互作用。（但这个假设其实有问题，因为研究者不是随机发现新链接的，新链接的发现会受到已发现链接的影响。在网络中有些部分被研究得更彻底，有些部分就几乎没有什么了解，不同部分的发现难度不同)

第二种假设可以以社交网络举例，随着时间流转，人们认识更多朋友。

基于相似性进行链接预测：计算两点间的相似性得分（如用共同邻居衡量相似性），然后将点对进行排序，得分最高的 n 组点对就是预测结果，与真实值作比

distance-based feature：两点间最短路径的长度

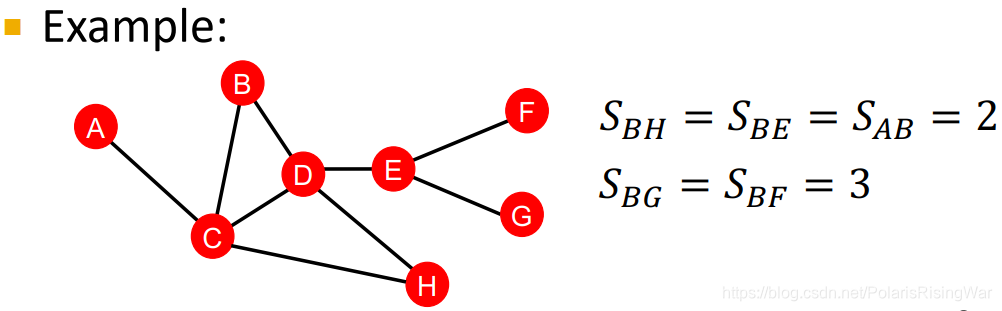
这种方式的问题在于没有考虑两个点邻居的重合度 the degree of neighborhood overlap，如 B-H 有 2 个共同邻居，B-E 和 A-B 都只有 1 个共同邻居。

local neighborhood overlap：捕获节点的共同邻居数

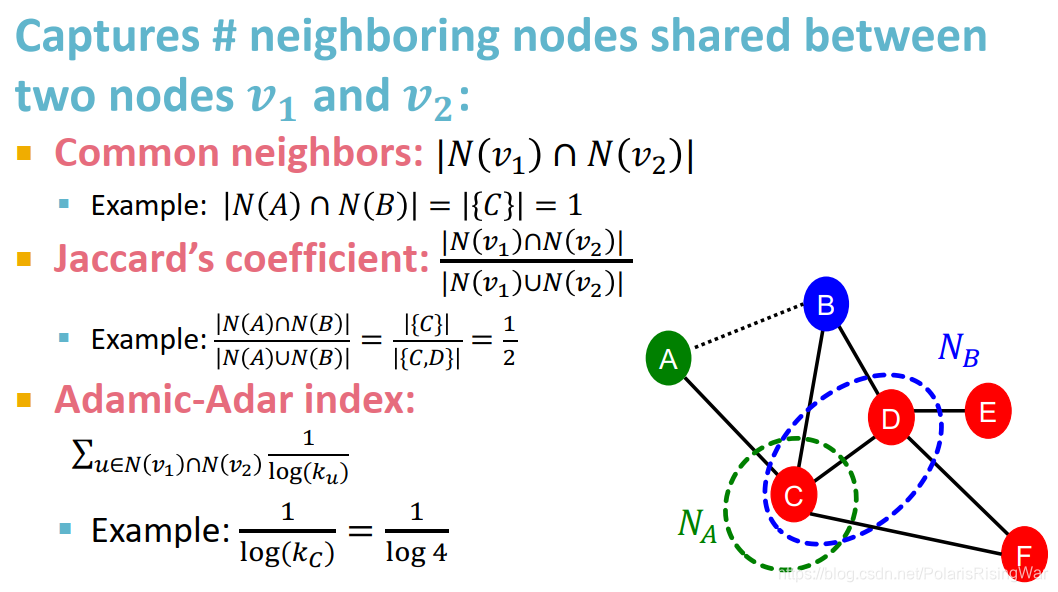
common neighbors 的问题在于度数高的点对就会有更高的结果，Jaccard’s coefficient 是其归一化后的结果。

Adamic-Adar index 在实践中表现得好。在社交网络上表现好的原因：有一堆度数低的共同好友比有一堆名人共同好友的得分更高。

global neighborhood overlap

local neighborhood overlap 的限制在于，如果两个点没有共同邻居，值就为 0。

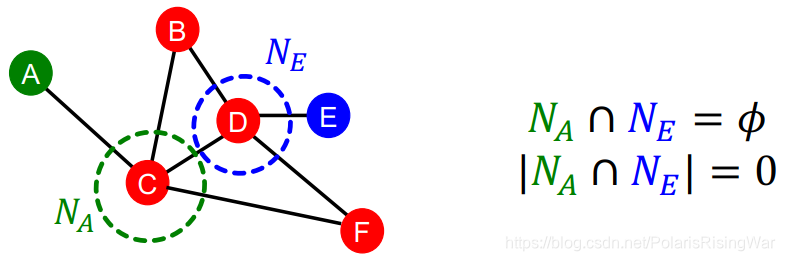
但是这两个点未来仍有可能被连接起来。所以我们使用考虑全图的 global neighborhood overlap 来解决这一问题。

Katz index：计算点对之间所有长度路径的条数

计算方式：邻接矩阵求幂

  1. 邻接矩阵的 k 次幂结果，每个元素就是对应点对之间长度为 k 的路径的条数

  2. 证明：

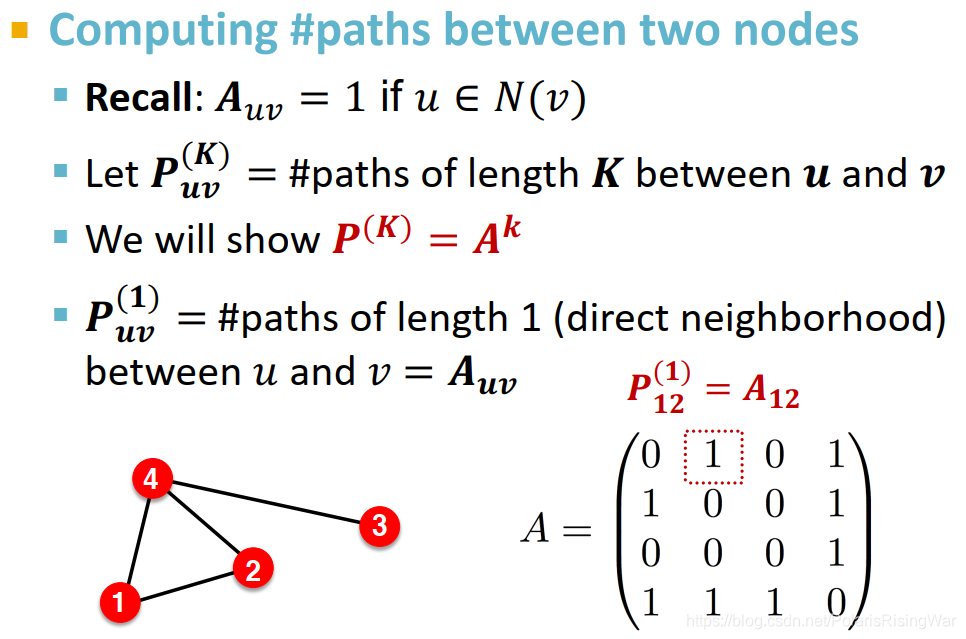
    显然 Auv\mathbf{A}_{uv}代表 u 和 v 之间长度为 1 的路径的数量

计算 uu 和 vv 之间长度为 2 的路径数量，就是计算每个 uu 的邻居 Aui\mathbf{A}_{ui}​ （与 uu 有 1 条长度为 1 的路径）与 vv 之间长度为 1 的路径数量 Piv(1)\mathbf{P}^{(1)}_{iv}​ 即 Aiv\mathbf{A}_{iv} 的总和 ∑iAui∗Aiv=Auv2\sum_i \mathbf{A}_{ui}*\mathbf{A}_{iv}=\mathbf{A}_{uv}^2​

同理，更高的幂（更远的距离)就重复过程，继续乘起来。从而得到 Katz index 的计算方式：

discount factor β\beta 会给比较长的距离以比较小的权重，exponentially with their length.

closed-form 闭式解，参考什么叫闭型（closed-form）？

解析解的推导方法，β\beta 是权重衰减因子，为了保证数列的收敛性，其取值需小于邻接矩阵A最大特征值的倒数。该方法权重衰减因子的最优值只能通过大量的实验验证获得，因此具有一定的局限性。

解析解推导过程：

矩阵形式的表达式为 S=βA+β2A2+β3A3…S=\beta A+\beta ^{2}A^{2}+\beta ^{3}A^{3}\ldots

(I−βA)(I+S)=(I−βA)(I+βA+β2A2+β3A3… )=(I+βA+β2A2+β3A3… )−(βA+β2A2+β3A3… )=I\begin{aligned} (I-\beta A)(I+S) &= (I−\beta A)(I+\beta A+\beta ^2A^2+\beta ^3A^3\dots) \\ &= (I+\beta A+\beta ^2A^2+\beta ^3A^3\dots)−(\beta A+\beta ^2A^2+\beta ^3A^3\dots)\\ &=I \end{aligned}

所以I+S=(I−βA)−1I+S=(I-\beta A)^{-1}，故S=(I−βA)−1−IS=(I-\beta A)^{-1}-I

Traditional Feature-based Methods: Graph

图级别特征构建目标：找到能够描述全图结构的特征。Background: Kernel Methods

核方法，相对复杂，pass

节点嵌入 Node Embedding

表征学习（representation learning）的目标是提供一个统一的图特征提取方式，对于不同的图机器学习任务都可以使用，而节点嵌入就是指将图中的节点映射到嵌入空间中，用一个稠密的向量来表示不同的节点，而向量的相似度又决定了节点在图中的相似度，也就是说将整个网络进行了编码。

目标就是让上面的f映射自动发生，自己被训练出来。并且得到的向量能够捕获他们感兴趣的底层网络的结构，用于预测。任务是将节点映射到嵌入空间，且节点之间的相似性就是它们在网络中的相似性。

Embedding

作用：将节点映射到一个 embedding 空间中。

下面是 embedding 的性质和作用：

  1. 网络中相似的节点，在 Embedding 空间中也是相似的。
  2. 潜在地被用来作为下游的预测
  3. 编码网络信息

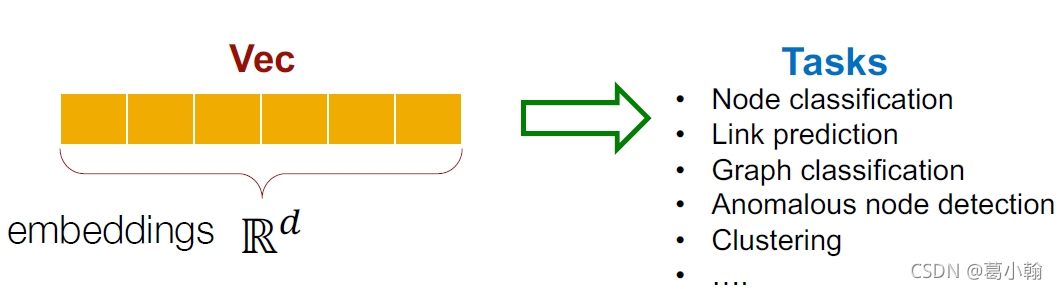
编码器和解码器

节点嵌入的目标就是对节点进行编码并映射到嵌入空间中，使得两个节点在嵌入空间中的相似度近似于节点在图中的相似度，而相似度和嵌入向量的形式都是需要定义的。因此节点嵌入的两个关键的组件就是编码器和相似度函数

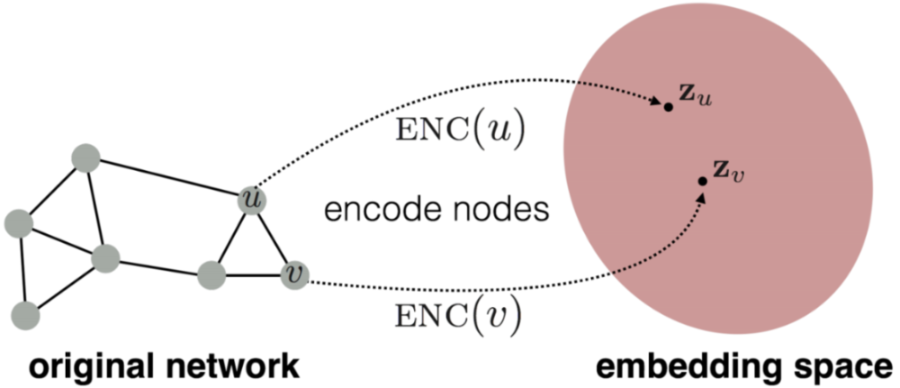
上图的目的是为了让 embedding 空间中的相似性近似图中的相似性，其中 embedding 空间一般是 D 维空间，相似性可以用向量 zuz_u和zvz_v的内积来衡量。如下图所示，节点在图中的相似性等于节点 embedding 之后的相似性，不过节点在图中的相似性需要定义

Node Embedding 涉及到的过程:

  1. 编码（Encoder）：将节点映射到 embedding 空间
  2. 在映射的过程中需要定义原始图中的节点相似性，以保证映射后的节点相似性有个优化目标。
  3. 解码（Decoder）：将 embedding 空间中的节点集映射为相似性得分。
  4. 优化编码参数以解码得分满足Goal所示的公式，其中解码得分使用内积的形式。

两个关键部分：

浅编码 Shallow Encoder

最简单的编码器的形式就是一个简单的嵌入映射，即将节点通过矩阵运算直接转化成对应的嵌入向量，可以表示为：ENC(v)=Z⋅vENC(v)=Z\cdot v

  • 其中 Z 就是一个d×∣v∣d\times|v|维度的矩阵，存储了每个节点的 d 维嵌入向量，而 v 就是一个 0-1 向量，除了对应的节点那一列是 1 以外都是 0
  • 我们需要学习的就是 Z 矩阵，这种编码器下面每个节点都映射到一个单独的嵌入向量中

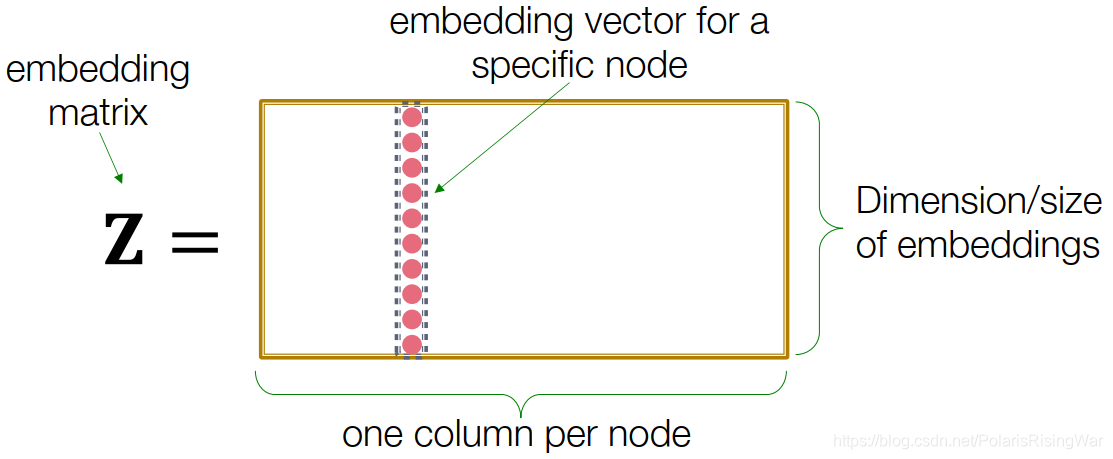
缺点：参数多，很难scale up到大型图上。

优点：如果获得了Z，各节点就能很快得到embedding。

有很多种方法：如DeepWalk，node2vec等

如何定义节点相似性

定义节点相似性的可能猜想，如果节点是相似的那么

  1. 两个节点是连接的？
  2. 有共享邻居节点？
  3. 有相似的结构表示？

后面将会用随机游走算法（random walks）来定义图节点的相似性，然后优化编码方式以近似图节点的相似结果。

节点嵌入的注意事项：

  • 学习节点嵌入是一个无监督 / 自监督的方法
    1. 不使用节点标签
    2. 不使用节点特征
    3. 节点嵌入的目的是直接估计节点的坐标以保证图结构的一些方面被保留
  • 这些嵌入是任务独立的
    1. 他们并不是针对一个特定的任务来训练，所以能够在其他任务中使用。

随机游走 Random Walk

统一符号表示notation

什么是随机游走

随机游走是一种用来定义图节点相似度的方法， zuz_u表示图节点 u 的嵌入向量，而概率P(v∣zu)P(v|\bold z_u)表示在节点 u 的随机游走中遇到节点 v 的概率。

随机游走的过程即每次随机选择当前节点的一个邻居并 “走” 到这个邻居的位置上不断重复的过程，这个过程中将产生一个随机的节点序列，称为图的随机游走。而用随机游走定义的相似度就是 uu 和 vv 出现在同一个随机游走中的概率。这种方式计算相似度需要以下几个步骤：

  • 使用一定的决策策略 R 来计算从 uu 出发的随机游走经过 vv 的概率
  • 根据随机游走的结果优化嵌入函数并进行编码

random walk embeddings

zuTzv≈\mathbf{z}_u^T\mathbf{z}_v\approx点 uu 和 vv 在一次随机游走中同时出现（点 vv 在以 uu 为起点的随机游走中出现）的概率

步骤如下，首先用随机游动策略 RR 估计从节点 uu 开始的随机游走中访问节点 vv 的概率。然后，优化这些 embedding 来编码随机游走统计参数。用 embedding 空间中的相似性（这个相似性需要专门的二元函数来计算，如简单的内积）来编码节点经过随机游走算法得出来的” 相似性 “.

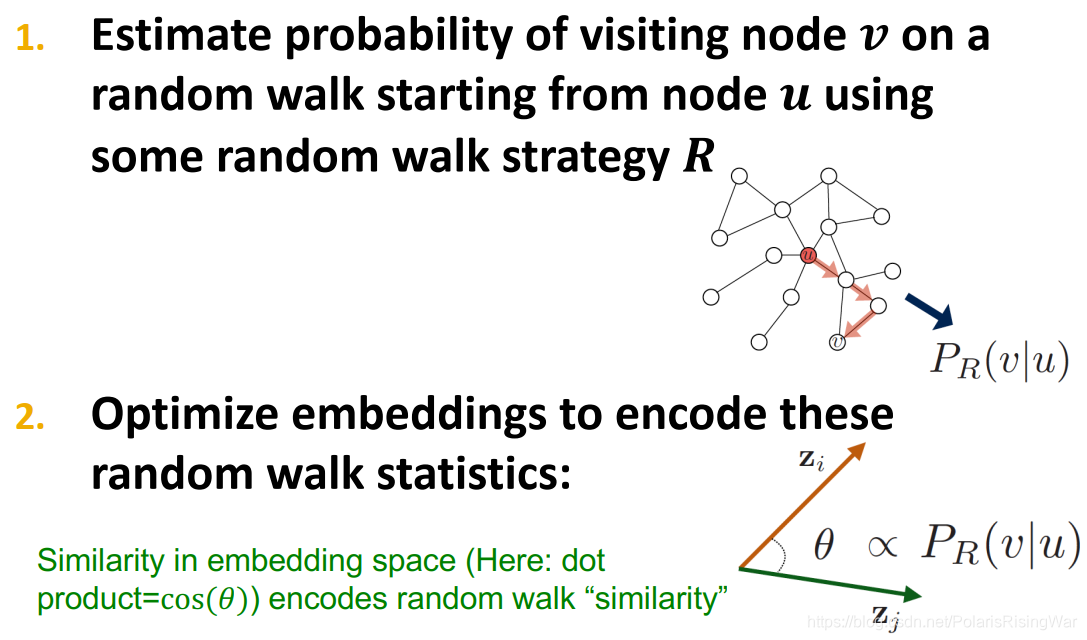
为什么需要随机游走

  • 可表达性：随机游走是一种灵活并且随机的相似度定义，并且包含了局部信息和更高阶的图中节点关系
  • 高效性：不需要在训练的过程中考虑所有的节点对，只需要考虑在随机游走中出现的节点对
  • 随机游走是一种无监督的特征学习

随机游走的优化

随机游走的目标是让学习到的嵌入向量中，相近的向量在图中更接近，对于一个节点 u 可以定义它在某种选择策略 R 下的随机游走中发现的邻居节点构成的集合是NR(u)N_R(u)，对于一个给定的图G=(V,E)G=(V,E)，我们的目标是学习出一个映射函数f(u)=zuf(u)=z_u，根据极大似然估计，我们的目标函数可以确定为：

max⁡f∑u∈Vlog⁡P(NR(u)∣zu)\max_f\sum_{u\in V}\log P(N_R(u)|z_u)

即对于给定的节点 u，我们希望通过随机游走中的表现来学习其特征的表示，而虽有游走可以进行一系列的优化，包括：

  • 进行一个较短的固定长度的随机游走

  • 对于每个节点 u 的邻居节点，允许邻居节点集合中出现重复的节点，出现的越多表明相似度越高, 因此最大化上述目标函数可以等价于最小化下面的表达式：

  • L=∑u∈V∑v∈NR(u)−log⁡(P(v∣zu))\mathcal{L}=\sum_{u\in V}\sum_{v\in N_R(u)}-\log(P(v|z_u))

而概率可以用 sotfmax 函数来进行参数化，选用 softmax 函数的原因是因为指数运算避免了负概率的出现，并且使得不同节点的相似度区分变得更加明显 ​

P(v∣zu)=exp⁡(zuTzv)∑n∈Vexp⁡(zuTzn)P(v|z_u)=\frac{\exp(z_u^Tz_v)}{\sum_{n\in V}\exp(z_u^Tz_n)}

问题在于这个双重求和的计算时间复杂度是 O(∣V∣2)O(|V|^2)，可以采用负采样的方式来近似计算损失函数，这里用到了 sigmoid 函数来近似计算。负采样简单来说就是原本我们是用所有节点作为归一化的负样本，现在我们只抽出一部分节点作为负样本，通过公式近似减少计算

log⁡(exp⁡(zuTzv)∑n∈Vexp⁡(zuTzn))≈log⁡(σ(zuTzv))−∑i=1klog⁡(σ(zuTzni))\begin{aligned}\log(\frac{\exp(z_u^Tz_v)}{\sum_{n\in V}\exp(z_u^Tz_n)})&\approx\log(\sigma(z_u^Tz_v))-\sum_{i=1}^k\log(\sigma(z_u^Tz_{n_i}))\end{aligned}

  • 这种近似方法不计算全部节点而是只采样了 K 个随机的负样本，并且用 sigmoid 函数来近似指数运算，这里的 k 个 negative nodes 按照其度数成正比的概率进行选取

  • 在得到了目标函数的近似形式之后，我们可以采用随机梯度下降法来对目标函数进行优化，定义

  • L(u)=∑v∈NR(u)−log⁡(P(v∣zu))\mathcal{L}^{(u)}=\sum_{v\in N_R(u)}-\log(P(v|z_u))

    • 对于一个节点 i，和所有的节点 j，计算其导数

    • 更新每一个向量 j 直到收敛

    • zj=zj−η∂L(i)∂zjz_j=z_j-\eta\frac{\partial\mathcal{L}^{(i)}}{\partial z_j}

node2vec

现在的问题就变成了如何确定随机游走的策略，上面已经提到的策略有固定长度，没有偏见的选择策略，而 node2vec 是一种有偏见的随机游走策略，这种策略更加灵活并且达到了局部和全局的平衡

  • 常见的采样邻近节点的方式有 BFS 和 DFS，而 BFS 更注重局部的邻居结构，DFS 则更偏向于全局

有偏见的随机游走

有偏见的定长随机游走策略 R 有两个参数，一个是返回参数 p，代表了返回到前一个节点，另一个参数是出入 (in-out) 参数 q，代表了随机游走过程中的 BFS 和 DFS 的比例

  • 有偏见的随机游走需要记录当前的游走路径是从那里来的，在参数 p 中表示
  • 每次走到新的节点的时候计算邻近节点的权重，选择权重最高 (这里的权重其实也就是代表了走到这个节点的概率，当然是没有标准化的概率) 的节点作为游走的下一个目的地

node2vec 算法框架

  • 计算随机游走的概率分布
  • 对每个节点 u，找到 r 条从 u 出发的不同的长度为 l 的随机游走
  • 使用随机梯度下降法来优化 node2vec

算法的特点：

  1. 线性时间复杂度
  2. 所有的 3 个步骤都可以独立并行计算。

其他的随机游走算法：

  1. Different kinds of biased random walks:
    1. Based on node attributes
    2. Based on learned weights
  2. Alternative optimization schemes
    1. Directly optimize based on 1-hop and 2-hop random walk probabilities
  3. Network preprocessing techniques
    1. Run random walks on modified versions of the original network

图嵌入

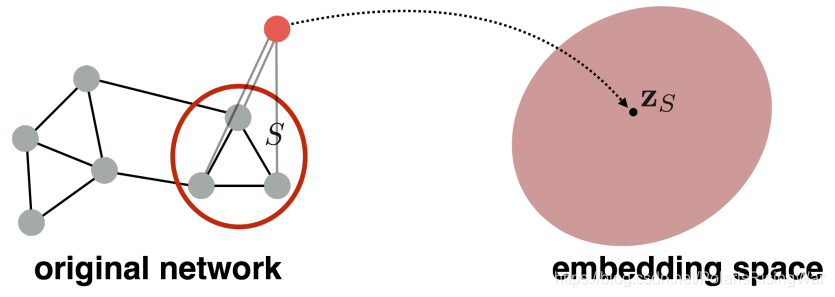
任务目标：嵌入子图或整个图 GG，得到表示向量 zG\mathbf{z}_G

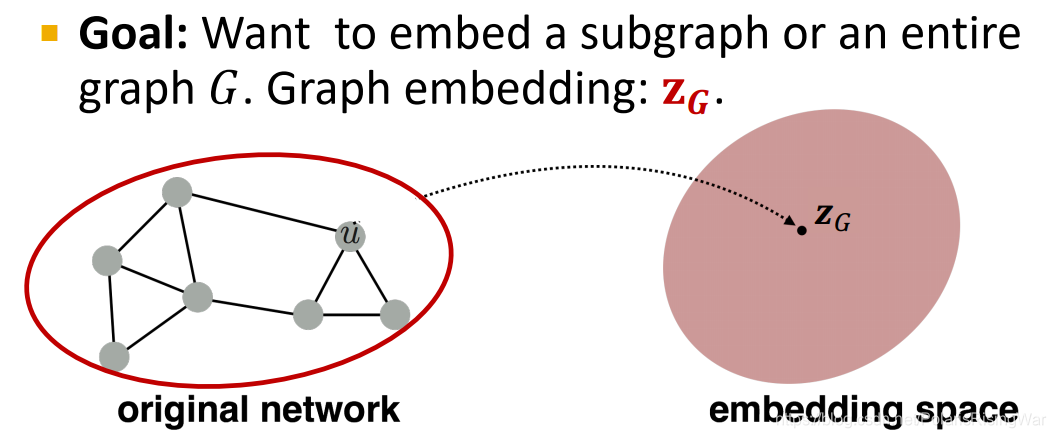
两种简单的 approach

  • 方法 1: 将图嵌入等价于图中所有节点的嵌入向量之和

  • ZG=∑v∈GzvZ_G=\sum_{v\in G}z_v

  • 方法 2: 在途中引入一个虚拟节点代表整个图 (子图) 并进行嵌入

  • 方法 3: 匿名游走嵌入

    • 想法 1: 对匿名游走进行采样并且用每种匿名游走的发生次数来表示一个图，也就是说用这些随机游走发生的概率来表示整张图，选定一个长度 L 之后，建立一个向量代表所有长度为 L 的随机游走发生的概率来代表这张图
    • 想法 2: 将匿名游走的嵌入结果进行合并

References

https://blog.csdn.net/PolarisRisingWar/article/details/117287320

https://zhang-each.github.io/

https://web.stanford.edu/class/cs224w/index.html